题目内容
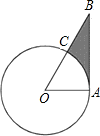 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是
- A.
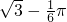
- B.
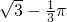
- C.
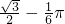
- D.
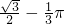
C
分析:在RT△OAB中,得出AB的长度,求出△OAB的面积,然后求出扇形OAC的面积,再由阴影部分的面积=三角形OAB的面积-扇形OAC的面积即可得出答案.
解答:∵AB是⊙O的切线,切点为A,
∴OA⊥AB,
在RT△OAB中,AB=OAtan∠AOB= ,
,
故S△OAB= OA•AB=
OA•AB= ,
,
S扇形OAC=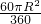 =
= ,
,
故可得:S阴影=S△OAB-S扇形OAC= -
- .
.
故选C.
点评:此题考查了扇形面积计算及切线的性质,属于基础题,解答本题的关键是判断出△OAB是直角三角形,难度一般.
分析:在RT△OAB中,得出AB的长度,求出△OAB的面积,然后求出扇形OAC的面积,再由阴影部分的面积=三角形OAB的面积-扇形OAC的面积即可得出答案.
解答:∵AB是⊙O的切线,切点为A,
∴OA⊥AB,
在RT△OAB中,AB=OAtan∠AOB=
 ,
,故S△OAB=
 OA•AB=
OA•AB= ,
,S扇形OAC=
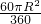 =
= ,
,故可得:S阴影=S△OAB-S扇形OAC=
 -
- .
.故选C.
点评:此题考查了扇形面积计算及切线的性质,属于基础题,解答本题的关键是判断出△OAB是直角三角形,难度一般.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
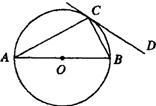 12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=
12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=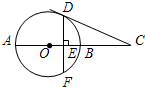 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )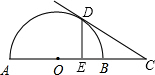
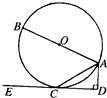 21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD.
21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD.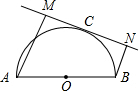 如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为
如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为