题目内容
【题目】如图，已知⊙O的半径OA的长为2，点B是⊙O上的动点，以AB为半径的⊙A与线段OB相交于点C，AC的延长线与⊙O相交于点D．设线段AB的长为x，线段OC的长为y．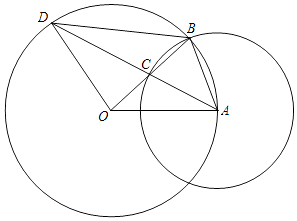 
（1）求y关于x的函数解析式，并写出定义域；
（2）当四边形ABDO是梯形时，求线段OC的长．
【答案】
（1）解：在⊙O与⊙A中，
∵OA=OB，AB=AC，
∴∠ACB=∠ABC=∠OAB，
∴△ABC∽△OAB，
∴ 
= 
，
∴ 
= 
，
∴BC= 
x2，
∵OC=OB﹣BC，
∴y关于x的函数解析式y=2﹣ x2，
定义域为0＜x＜2．
（2）解：①当OD∥A B时，
∴ 
= 
，
∴ 
= 
，
整理得x2+2x﹣4=0，
∴x=﹣1 
（负值舍去），
∴AB= 
，这时AB≠OD，符合题意．
∴OC=2﹣ x2=2﹣ （ 
﹣1）2= 
﹣1．
②当BD∥OA时，设∠ODA=α，
∵BD∥OA，OA=OD，
∴∠BDA=∠OAD=∠ODA=α，
又∵OB=OD，∴∠BOA=∠OBD=∠ODB=2α，
∵AB=AC，OA=OB，
∴∠OAB=∠ABC=∠ACB=∠COA+∠CAO=3α，
∵∠AOB+∠OAB+∠OBA=180°，
∴2α+3α+3α=180°，
∴α=22.5°，∠BOA=45°，
∴∠ODB=∠OBD=45°，∠BOD=90°，
∴BD=2 
，
∵BD∥OA，
∴ = 
，
∴ 
= 
，
∴y=2 ﹣2．OC=2 ﹣2，
由于BD≠OA，OC=2 
﹣2符合题意．
∴当四边形ABDO是梯形时，线段OC的长为 
﹣1或2 ﹣2．
【解析】（1）由△ABC∽△OAB，推出 
= 
，可得 
= 
，推出BC= 
x2，由OC=OB﹣BC，可得y关于x的函数解析式y=2﹣ x2；（2）分两种情形讨论①当OD∥A B时，②当BD∥OA时，分别想办法构建方程解决问题；
