题目内容
(本小题满分12分)如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
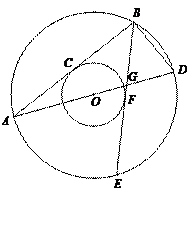
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求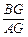 的值.
的值.
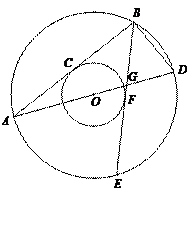
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求
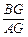 的值.
的值.解:(1)连接OC,并延长BO交AE于点H,
∵AB是小圆的切线,C是切点,
∴OC⊥AB,
 ∴C是AB的中点.
∴C是AB的中点.
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD=2OC=10.
(2)连接AE,由(1)知C是AB的中点.
同理F是BE的中点.
由切线长定理得BC=BF.
∴BA=BE.
∴∠BAE=∠E.
∵∠E=∠D,
∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180º.
(3)连接BO,在Rt△OCB中,
∵OB=13,OC=5,
∴BC=12.
由(2)知∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB.
∴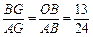 .
.
∵AB是小圆的切线,C是切点,
∴OC⊥AB,
 ∴C是AB的中点.
∴C是AB的中点. ∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD=2OC=10.
(2)连接AE,由(1)知C是AB的中点.
同理F是BE的中点.
由切线长定理得BC=BF.
∴BA=BE.
∴∠BAE=∠E.
∵∠E=∠D,
∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180º.
(3)连接BO,在Rt△OCB中,
∵OB=13,OC=5,
∴BC=12.
由(2)知∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB.
∴
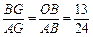 .
. 略

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
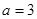 cm,
cm,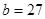 cm,则线段
cm,则线段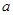 ,
,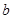 的比例中项为 cm.
的比例中项为 cm.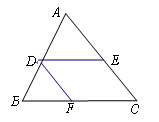
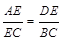
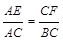
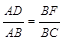
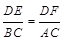
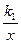 (k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=
(k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=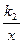 (0<k2<︱k1︱)于E,F两点.
(0<k2<︱k1︱)于E,F两点.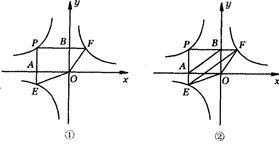
 ( )
( )
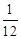
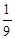
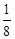
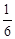
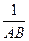 +
+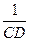 =
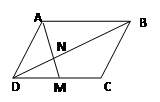
=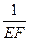 成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交于点E,过点E作EF∥AB交BD于F,则
成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交于点E,过点E作EF∥AB交BD于F,则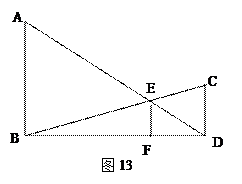

 , 则
, 则 ▲ .
▲ .