题目内容
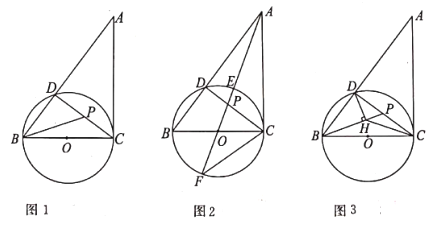
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
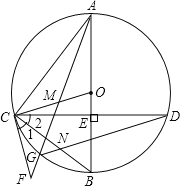
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.
【答案】(1)见解析(2)见解析(3)![]()
【解析】解:(1)证明:∵△BCO中,BO=CO,∴∠B=∠BCO。
在Rt△BCE中,∠2+∠B=900,∠1=∠2,∴∠1+∠BCO=900,即∠FCO=90°。
∵OC是⊙O的半径,∴CF是⊙O的切线。
(2)证明:∵AB是⊙O直径,∴∠ACB=∠FCO=900。
∴∠ACB-∠BCO=∠FCO-∠BCO,即∠3=∠1。
∴∠3=∠2。
∵∠4=∠D,∴△ACM∽△DCN。
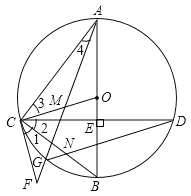
(3)∵⊙O的半径为4,即AO=CO=BO=4,
在Rt△COE中,cos∠BOC=![]() ,
,
∴OE=COcos∠BOC=4×![]() =1。∴BE=3,AE=5。
=1。∴BE=3,AE=5。
由勾股定理可得:![]() ,
,
![]() 。
。
∵AB是⊙O直径,AB⊥CD,∴由垂径定理得:CD=2CE=![]() 。
。
∵点M是CO的中点,∴CM=![]() CO=
CO=![]() ×4=2
×4=2
∵△ACM∽△DCN,∴![]() ,即
,即![]() 。
。
∴![]() 。
。
(1)根据切线的判定定理得出∠1+∠BCO=900,即可得出答案;
(2)利用已知得出∠3=∠2,∠4=∠D,再利用相似三角形的判定方法得出即可。
(3)根据已知得出OE的长,从而利用勾股定理得出EC,AC,BC的长,即可得出CD,利用(2)中相似三角形的性质得出NB的长即可。

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案【题目】2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情.为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传.某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析,过程如下:
(收集数据)
甲班15名学生测试成绩分别为:78,83,89,97,98,85,100,94,87,90,93,92,99,95;100.
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
(整理数据):
班级 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
甲 | 1 | 1 | 3 | 4 | 6 |
乙 | 1 | 2 | 3 | 5 | 4 |
(分析数据):
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 92 | a | 93 | 47.3 |
乙 | 90 | 87 | b | 50.2 |
(应用数据):
(1)根据以上信息,可以求出:a=_____分,b=______分;
(2)若规定测试成绩92分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).