题目内容
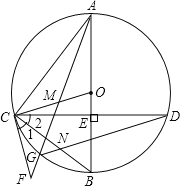
【题目】如图，在
中，已知：
，
，
，以斜边AB的中点P为旋转中心，把这个三角形按逆时针方向旋转
得到
，则旋转前后两个直角三角形重叠部分的面积为__________
．
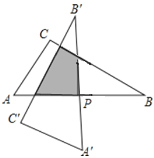
【答案】
【解析】
如图，在Rt△DPB中， 根据勾股定理求得DP=
，再证明△B′PH≌△BPD，根据全等三角形的性质可得PH=PD=；在直角△BGH中，BH=3+，可求得GH=
，BG=
（3+），根据SDGHP= S△BGH- S△BDP即可求得重合部分的面积.
如图，在直角△DPB中，BP=AP=AC=3，设DP=x，
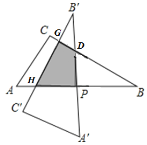
∵∠A=60°，
∴DP2+BP2=BD2，
∴x2+32=（2x）2，
∴DP=x=，
∵在△B′PH和△BPD中，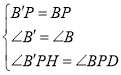
，
∴△B′PH≌△BPD，
∴PH=PD=，
∵在直角△BGH中，BH=3+，
∴GH=，BG=（3+），
∴S△BGH=
××（3+）=
，S△BDP=×3×=
，
∴SDGHP=-=cm2．
故答案为．
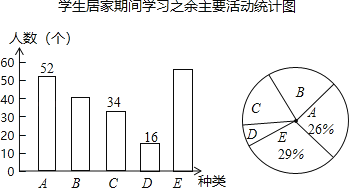
【题目】为普及防治新型冠状病毒感染的科学知识和有效方法，不断增强同学们的自我保护意识，学校举办了新型冠状病毒疫情防控网络知识竞答活动，试卷题目共10题，每题10分．现分别从七年级的三个班中各随机取10名同学的成绩（单位：分），收集数据如表：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100．
整理数据：
分数 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 | a | 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据：
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | |
2班 | 83 | c | d |
3班 | b | 80 | 80 |
根据以上信息回答下列问题：
（1）请直接写出表格中a，b，c，d的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；
（3）为了让同学们重视疫情防控知识的学习，学校将给竞答成绩满分的同学颁发奖状，该校七年级新生共600人，试估计需要准备多少张奖状？
