Question

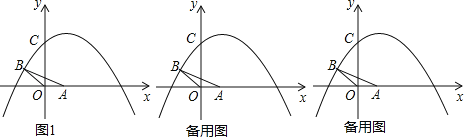
【题目】如图1，平面直角坐标系中，△OAB的边OA在x轴的正半轴上，点B在第二象限，且∠AOB=135°，OA=2，OB=2，抛物线y=﹣x2+bx+c经过点B，并与y轴交于点C（0，5），点P在抛物线的对称轴上．

（1）求b、c的值，及抛物线的对称轴．

（2）求证：以点M（2，5）为圆心，半径为2的圆与边AB相切．

（3）若满足条件∠AOB+∠POD=180°与OB：OD=OA：OP的点D恰好在抛物线上，请求出此时点P的坐标．

Answer 1

【答案】（1）1，5，；（2）见解析；（3）点P的坐标为（2，﹣2+2）或（2，﹣2﹣2）或（2，﹣8）或（2，4）．

【解析】

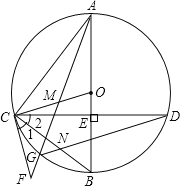
（1）如图1中，作BH⊥x轴于H．解直角三角形求出点B的坐标，利用待定系数法即可解决问题．

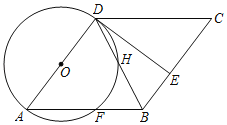
（2）如图2中，作MJ⊥AB于点J．求出直线AB，MJ的解析式，发现这两条直线的交点J在y轴上，求出MJ与半径比较即可解决问题．

（3）由题意∠POD=45°，OD：OP=OB：OA=，过点P作DP⊥OP，且PD=PD′=OP，连接OD，OD′，则点D和点D′满足条件，设P（2，m），则D（2﹣m，m+2），D′（2+m，m﹣2），利用待定系数法构建方程求出m即可解决问题．

（1）解：如图1中，作BH⊥x轴于H．

∵∠AOB=135°，

∴∠BOH=45°，

∵∠OHB=90°，OB=2，

∴BH=OH=2，

∴B（﹣2，2），

∵抛物线y=﹣x2+bx+c经过点B，并与y轴交于点C（0，5），

∴，

解得，

∴抛物线的解析式为y=﹣x2+x+5，

∴抛物线的对称轴x=﹣=2．

（2）证明：如图2中，作MJ⊥AB于J．

∵A（2，0），B（﹣2，2），

∴直线AB的解析式为y=﹣x+1，

∵M（2，5），MJ⊥AB，

∴直线MJ的解析式为y=2x+1，

∵直线AB交y轴于（0，1），直线MJ交y轴于（0，1），

∴J（0，1），

∴MJ==2，

∵⊙M的半径为2，

∴MJ=r，

∴⊙M与直线AB相切．

（3）解：∵∠AOB+∠POD=180°，∠AOB=135°，

∴∠POD=45°

∵OB：OD=OA：OP，

∴OD：OP=OB：OA=，

过点P作DP⊥OP，且PD=PD′=OP，连接OD，OD′，则点D和点D′满足条件，

设P（2，m），则D（2﹣m，m+2），D′（2+m，m﹣2），

当D（2﹣m，m+2）在y=﹣x2+x+5上时，m+2=﹣（2﹣m）2+2﹣m+5，

解得m=﹣2±2，

此时P（2，﹣2+2）或（2，﹣2﹣2），

当D′（2+m．m﹣2）在y=﹣x2+x+5时，m﹣2=﹣（2+m）2+2+m+5，

解得m=﹣8或4．

此时P（2，﹣8）或（2，4），

综上所述，满足条件的点P的坐标为（2，﹣2+2）或（2，﹣2﹣2）或（2，﹣8）或（2，4）．