题目内容
【题目】【问题情境】
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长
最小？最小值是多少？
【数学模型】
设该矩形的长为x，周长为y，则y与x的函数表达式为y=2（x+ 
）（x＞0）．
【探索研究】
小彬借鉴以前研究函数的经验，先探索函数y=x+ 
的图象性质．
（1）结合问题情境，函数y=x+ 的自变量x的取值范围是x＞0，如表是y与x的几组对应值．
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值；
②画出该函数图象，结合图象，得出当x=时，y有最小值，y最小=；
（2）【解决问题】
直接写出“问题情境”中问题的结论．
【答案】
（1）1；2
（2）
解：当 
时，y有最小值，即 
时， 
【解析】（1）解：①当y=4 
时，x=4，
∴m=4；∴函数y=x+ 
（x＞0）的图象如图．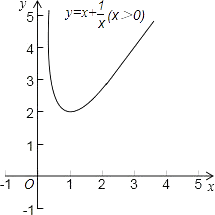
②当0＜x＜1时，y随x增大而减小；当x＞1时，y随x增大而增大；当x=1时函数y=x+ （x＞0）的最小值为2．
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质，需要了解一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远才能得出正确答案．
练习册系列答案
相关题目
