题目内容
【题目】如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1
B.1∶2∶3
C.2∶3∶4
D.3∶4∶5
【答案】C
【解析】解:过点O作OE⊥AB于点E,OF⊥BC于点F,OD⊥AC于点D,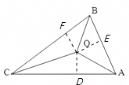
∵OA,OB,OC分别是△ABC三内角的角平分线,
∴OE=OF=OD ,
∵S△ABO=![]() AB·OE =10OE, S△BCO=
AB·OE =10OE, S△BCO=![]() BC·OF=15OF ,S△CAO=
BC·OF=15OF ,S△CAO=![]() AC·OD=20OD,
AC·OD=20OD,
∴S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4
故应选:C.
根据角平方线上的点到角两边的距离相等得出OE=OF=OD ,根据三角形的面积法,得出S△ABO=![]() AB·OE =10OE, S△BCO=
AB·OE =10OE, S△BCO=![]() BC·OF=15OF ,S△CAO=
BC·OF=15OF ,S△CAO=![]() AC·OD=20OD,从而得出答案S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4 。
AC·OD=20OD,从而得出答案S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4 。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目