题目内容
【题目】如图,BP,CP分别是△ABC的外角平分线,且相交于点P.求证:点P在∠BAC的平分线上.
【答案】证明:过点P分别作PE⊥AB于E,PF⊥AC于F,PG⊥BC于G;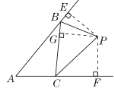
.∵BP,CP分别是△ABC的外角平分线,
∴PE=PG,PG=PF,
则PE=PF.
∴点P在∠BAC的平分线上.
【解析】过点P分别作PE⊥AB于E,PF⊥AC于F,PG⊥BC于G;根据角平分线上的点到角两边的距离相等得出PE=PG,PG=PF,进而得到PE=PF.根据角平分线的判定定理,到角两边距离相等的点在这个角的角平分线上得出点P在∠BAC的平分线上.
【考点精析】认真审题,首先需要了解角的平分线判定(可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)),还要掌握角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上)的相关知识才是答题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目