��Ŀ����
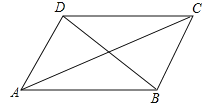
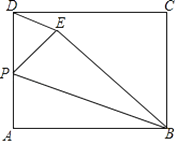
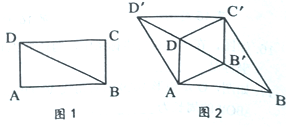
����Ŀ����ͼl��BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30![]() ��AD=1������BCD������BD����ƽ�Ƶ���B'C'D'��λ�ã�ʹB'ΪBD�е㣬����AB����C'D��AD����BC������ͼ2��
��AD=1������BCD������BD����ƽ�Ƶ���B'C'D'��λ�ã�ʹB'ΪBD�е㣬����AB����C'D��AD����BC������ͼ2��
(1)��֤���ı���AB'C'D�����Σ�
(2)�ı���ABC'D'���ܳ�Ϊ____��
(3)���ı���ABC'D�������������Խ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д������ƴ�ɵľ��ε��ܳ�.
���𰸡���1��֤������������2��4![]() ����2��3+2
����2��3+2![]() ��6+
��6+![]()
�������������������1����һ���ڱ���ȵ�ƽ���ı��������Σ��ݴ˽���֤�����ɣ�
��2�����ж��ı���ABC'D'�����Σ��ٸ��ݱ߳�AB=![]() AD=
AD=![]() �����ɵõ��ı���ABC'D�����ܳ�Ϊ4
�����ɵõ��ı���ABC'D�����ܳ�Ϊ4![]() ��
��
��3���������ֲ�ͬ��ƴ�����ֱ���ÿ���ƴ�ɵľ����ܳ�
�����������1����BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30����
���ADB=60����
��ƽ�ƿɵã�B'C'=BC=AD����D'B'C'=��DBC=��ADB=60����
��AD��B'C'
���ı���AB'C'D��ƽ���ı��Σ�
��B'ΪBD�е㣬
��Rt��ABD��AB'=![]() BD=DB'��
BD=DB'��
���ߡ�ADB=60����
���ADB'�ǵȱ������Σ�
��AD=AB'��
���ı���AB'C'D�����Σ�
��2����ƽ�ƿɵã�AB=C'D'����ABD'=��C'D'B=30����
��AB��C'D'��
���ı���ABC'D'��ƽ���ı��Σ�
�ɣ�1���ɵã�AC'��B'D��
���ı���ABC'D'�����Σ�
��AB=![]() AD=
AD=![]() ��
��
���ı���ABC'D�����ܳ�Ϊ4![]() ��
��
��3�����ı���ABC'D'�����������Խ��������õõ����ĸ�������ƴ�����������ȵľ������£�
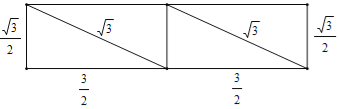
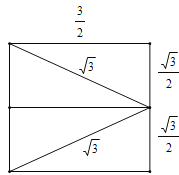
�������ܳ�Ϊ6+![]() ��2
��2![]() +3��
+3��

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�