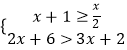题目内容
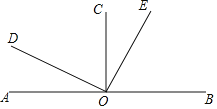
【题目】如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE=![]() ∠BOD.
∠BOD.
(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.
【答案】(1)120°;(2)150°
【解析】
试题(1)由于∠COE=![]() ∠BOD,可设∠COE=x,则∠BOD=5x,列出方程即可求出x的值,进而求出∠COE,∠BOD,∠AOE的度数.
∠BOD,可设∠COE=x,则∠BOD=5x,列出方程即可求出x的值,进而求出∠COE,∠BOD,∠AOE的度数.
(2)作出∠BOE的角平分线后求出∠BOF的度数即可求出∠AOF的度数.
解: (1)∵∠COE=![]() ∠BOD
∠BOD
∴设∠COE=x,则∠BOD=5x
∵OD⊥OE, ∴∠DOE=90°,
∴∠BOE=∠BOD-∠DOE=5x-90°
∵OC⊥AB, ∴∠BOC=90°, ∴∠COE+∠BOE=90°
∴x+5x-90=90, x=30°
∴∠COE=30°
∴∠BOD=5x=150°
∴∠AOE=∠AOC+∠COE=90+30=120°
(2)作OF平分∠BOE
∴∠BOF=![]() ∠BOE
∠BOE
∵∠BOE=90°-∠COE=60°, ∴∠BOF=30°
∴∠AOF=180°-∠BOF=150°

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目