题目内容
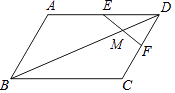
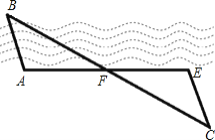
【题目】如图,小明和小月两家位于A,B两处隔河相望,要测得两家之间的距离,小明设计方案如下:
①从点A出发沿河岸画一条射线AM;
②在射线AM上截取AF=FE;
③过点E作EC∥AB,使B,F,C在一条直线上;
④CE的长就是A,B间的距离.
(1)请你说明小明设计的原理.
(2)如果不借助测量仪,小明的设计中哪一步难以实现?
(3)你能设计出更好的方案吗?
【答案】(1)全等三角形的对应边相等;(2)③难以实现;(3)见解析 (答案不唯一,只要设计合理即可).
【解析】
(1)利用了证明全等三角形边角边的设计原理;
(2)如果不借助测量仪,小明和小月无法使得EC∥AB;
(3)还可以利用相似三角形原理即可,这样所要的空间较少.
(1)∵EC∥AB,
∴∠CEF=∠BAF,
∵AF=FE,∠BFA=∠EFC,
∴△BAF≌△CEF(ASA),
∴小明和小月运用了全等三角形(边角边)原理;
(2)如果不借助测量仪,小明和小月无法使得EC∥AB;
(3)还可以这样设计: ①从点A出发沿河画一条射线AE; ②在AE上截取AF=5FE; ③过E作EC∥AB,使得B,F,C点在同一直线上;④则CE的5倍的长就是AB之间的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目