题目内容
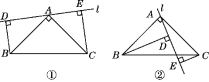
【题目】如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.
(1)试说明:DE=BD+CE.
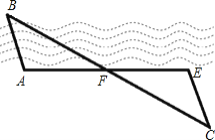
(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.
【答案】(1) 见解析; (2)(1)中结论不成立.DE=BD-CE. 探究过程见解析.
【解析】
(1)由AAS证明△ABD≌△CAE,得到BD=AE,AD=CE,即可解决问题.(2)由AAS证明证明△ABD≌△CAE,得出BD=AE,AD=CE,即可得出结论.
(1)因为BD⊥l,CE⊥l,
所以∠ADB=∠AEC=90°.
所以∠DBA+∠BAD=90°.
又因为∠BAC=90°,
所以∠BAD+∠CAE=90°.
所以∠DBA=∠CAE.
因为AB=AC,∠ADB=∠CEA=90°,
所以△ABD≌△CAE(AAS).
所以AD=CE,BD=AE.
则AD+AE=BD+CE,
即DE=BD+CE.
(2)(1)中结论不成立.
DE=BD-CE.
同(1)说明△ABD≌△CAE,
所以BD=AE,AD=CE.
又因为AE-AD=DE,
所以DE=BD-CE.

练习册系列答案
相关题目