题目内容
【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)欲证明AD=CE,只要证明△ABD≌△CBE即可;
(2)如图2中,倍长BE到H,连CH,DH.首先证明△DBH是等边三角形,由(1)可知,△ABD≌△CBH,推出AD=CH,∠A=∠HCB=∠ABC=60°,推出BF∥CH,推出∠F=∠ECH,再证明△EBF≌△EHC,推出BF=CH,由此即可证明.
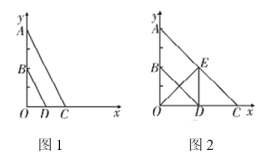
(1)证明:如图1中,
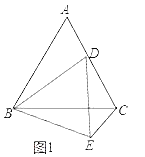
∵△ABC,△BDE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中, 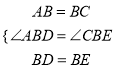 ,
,
∴△ABD≌△CBE,
∴AD=CE.
(2)如图2中,倍长BE到H,连CH,DH.
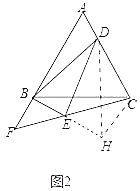
∵BE=EH,DE⊥BH,
∴DB=DH,∠BDE=∠HDE=30°,
∴∠BDH=60°,
∴△DBH是等边三角形,
由(1)可知,△ABD≌△CBH,
∴AD=CH,∠A=∠HCB=∠ABC=60°,
∴BF∥CH,
∴∠F=∠ECH,
在△EBF和△EHC中, 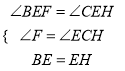 ,
,
∴△EBF≌△EHC,
∴BF=CH,
∴AD=CE.

 小学夺冠AB卷系列答案
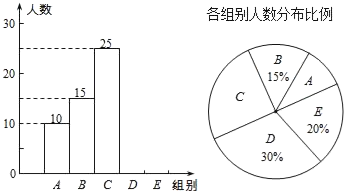
小学夺冠AB卷系列答案【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.