题目内容
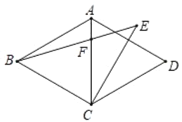
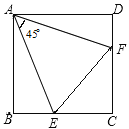
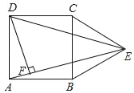
【题目】如图，在正方形ABCD的外侧，作等边三角形BCE，连接AE，DE．
（1）求证：AE＝DE
（2）过点D作DF⊥AE，垂足为F，若AB＝2cm，求DF的长．
【答案】（1）详见解析；（2）
【解析】
（1）证明△ABE≌△DCE，可得结论；
（2）作辅助线，构建直角三角形，根据等腰三角形的性质得∠BCG＝30°，∠DEF＝30°，利用正方形的边长计算DE的长，从而得DF的长．
（1）证明：∵四边形ABCD是正方形，
∴AB＝CD，∠ABC＝∠DCB＝90°，
∵△BCE是等边三角形，
∴BE＝CE，∠EBC＝∠ECB＝60°，
即∠ABE＝∠DCE＝150°，
∴△ABE≌△DCE，
∴AE＝DE；
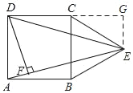
（2）解：过点E作EG⊥CD于G，
∵DC＝CE，∠DCE＝150°，
∴∠CDE＝∠CED＝15°，
∴∠ECG＝30°，
∵CB＝CD＝AB＝2，
∴EG＝1，CG＝
，
在Rt△DGE中，DE＝
，
在Rt△DEF中，∠EDA＝∠DAE＝90°﹣15°＝75°
∴∠DEF＝30°，
∴DF＝
DE＝
（cm）．
练习册系列答案
名校课堂系列答案
相关题目
