题目内容
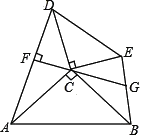
【题目】如图,等腰![]() 与等腰
与等腰![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转,则
顺时针旋转,则![]() 的长的最大值是______.
的长的最大值是______.
【答案】![]()
【解析】
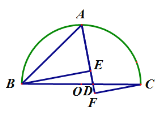
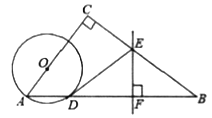
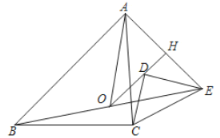
延长ED到N,使得DN=DE,连接CN,BN,延长BN交AE于M.取BC的中点F,连接AF,OF.利用矩形的性质证明OD∥BN,推导出OB=OE,求出OF,AF即可解决问题.
如图,延长ED到N,使得DN=DE,连接CN,BN,延长BN交AE于M.取BC的中点F,连接AF,OF.
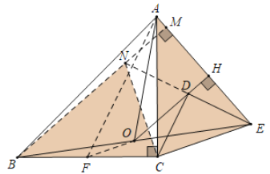
∵CD⊥EN,DN=DE,
∴CN=CE,
∵DC=DE,∠CDE=90°,
∴∠DCE=∠DCN=45°,
∴∠ACB=∠NCE=90°,
∴∠BCN=∠ACE,
在△BCN和△ACE中,
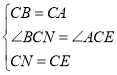 ,
,
∴△BCN≌△ACE(SAS),
∴∠BNC=∠AEC,
∵∠BNC+∠CNM=180°,
∴∠CNM+∠AEC=180°,
∴∠ECN+∠NME=180°,
∵∠ECN=90°,
∴∠NME=90°,
∵DH⊥AE,
∴∠NME=∠DHE=90°,
∴OD∥BN,
∵DN=DE,
∴OB=OE,
∵BF=CF,
∴OF=![]() EC,
EC,
∵CD=DE=6,∠CDE=90°,
∴EC=6![]() ,
,
∴OF=3![]() ,
,
在Rt△ACF中,∵AC=12,CF=6,
∴![]() ,
,
∵OA≤AF+OF,
∴OA≤6![]() +3
+3![]() ,
,
∴OA的最大值为6![]() +3
+3![]() .
.
故答案为6![]() +3
+3![]() .
.

练习册系列答案
相关题目