题目内容
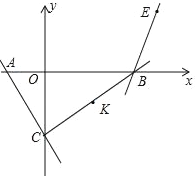
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,在平面内有一点E,其坐标为(4,
交x轴于点B,在平面内有一点E,其坐标为(4,![]() ),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移
),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
【答案】![]()
【解析】
由解析式求出A、B、C点坐标,进而求得K的坐标,关键平移的规律求得K′的坐标,将K′向右平移1个单位得到H,作H关于x轴的对称点H′,连接EH′交x轴于N,此时四边形K′MNE的周长最小.求出直线EH′的解析式即可解决问题.
∵直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,
交x轴于点B,
∴A(﹣1,0),
∴B(3,0),C(0,﹣![]() ),
),
∵K是BC中点,
∴k(![]() ,﹣
,﹣![]() ),
),
∵将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,
个单位得K′,
∴K′(1,![]() ),
),
如图,将K′向右平移1个单位得到H,作H关于x轴的对称点H′,连接EH′交x轴于N,此时四边形K′MNE的周长最小.
∵H(2,![]() ),H′(2,﹣
),H′(2,﹣![]() ),
),
∴直线EH′的解析式为y=![]() x﹣
x﹣![]() ,
,
令y=0,得到x=![]() ,
,
∴N(![]() ,0),
,0),
∴a=![]() ﹣1=
﹣1=![]() .
.

练习册系列答案
相关题目