��Ŀ����
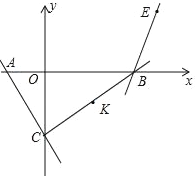
����Ŀ��С������ѧϰС����̽����ת��ƽ�Ʊ任����ͼ��ABC��DEF��Ϊ����ֱ�������Σ�����������ֱ�ΪA��1��1����B��2��2����C��2��1����D�� ![]() ��0����E��2
��0����E��2 ![]() ��0����F��
��0����F�� ![]() ����
���� ![]() ����
����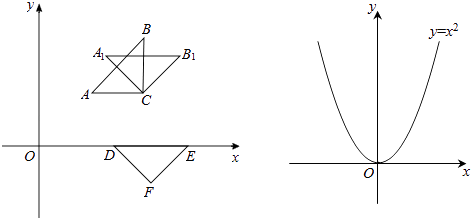
��1�����ǽ���ABC��C�㰴˳ʱ�뷽����ת45��õ���A1B1C1 �� ����д����A1 �� B1�����꣬���ж�A1C��DF��λ�ù�ϵ��
��2�����ǽ���ABC��ԭ�㰴˳ʱ�뷽����ת45�㣬������ת���������ǡ����������������������y=2 ![]() x2+bx+c�ϣ�����������������������߽���ʽ��
x2+bx+c�ϣ�����������������������߽���ʽ��
��3�����Ǽ���̽�������ֽ���ABC��ij������ת45�㣬����ת���������ǡ����������������������y=x2�ϣ���������ת�������ε�ֱ�Ƕ���P�����꣬����ֱ��д����P���������꣮
���𰸡�
��1��
�⣺A1��2�� ![]() ��1+
��1+ ![]() ����B1��2+
����B1��2+ ![]() ��1+
��1+ ![]() ����
����
A1C��DF��λ�ù�ϵ��ƽ��
��2��
�⣺�ߡ�ABC��ԭ�㰴˳ʱ�뷽����ת45���������μ�Ϊ��DEF��
��ٵ������߾�����D��Eʱ����������ɵã�
![]() ��
��
��� ![]()
��y= ![]() x2��12x+
x2��12x+ ![]() ��
��
�ڵ������߾�����D��Fʱ����������ɵã�
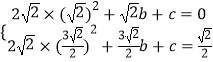 ��
��
��� ![]()
��y= ![]() x2��11x+
x2��11x+ ![]() ��
��
�۵������߾�����E��Fʱ����������ɵã�
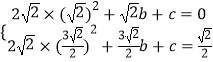 ��
��
��� ![]()
��y= ![]() x2��13x+
x2��13x+ ![]()
��3��
�⣺����ת�����У��������������Σ�
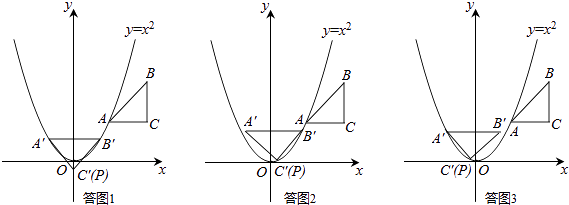
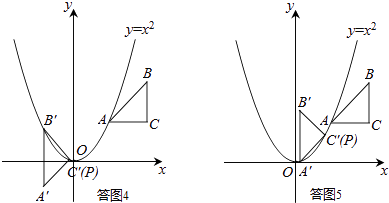
��˳ʱ����ת45�㣬��A��B�����������ϣ����ͼ1��ʾ��
����õ�P����Ϊ��0�� ![]() ����
����
��˳ʱ����ת45�㣬��B��C�����������ϣ����ͼ2��ʾ��
���B�䣬C��ĺ�����ֱ�Ϊx1��x2��
��֪��ʱB��C����һ��������ƽ����ƽ�У�����ֱ��B��C��Ľ���ʽΪy=x+b��
����y=x2��y=x+b�ã�x2=x+b����x2��x��b=0��
��x1+x2=1��x1x2=��b��
��B��C��=1������������ã�|x1��x2|= ![]() ��
��
�ࣨx1��x2��2= ![]() ������x1+x2��2��4x1x2=
������x1+x2��2��4x1x2= ![]()
��1+4b= ![]() �����b=-
�����b=- ![]() ��
��
��x2��x+ ![]() =0�����x=
=0�����x= ![]() ��x=
��x= ![]() ��
��
�ߵ�C��ĺ������С����x= ![]() ��
��
��x= ![]() ʱ��y=x2=
ʱ��y=x2= ![]() ��
��
��P�� ![]() ��
�� ![]() ����
����
��˳ʱ����ת45�㣬��C��A�����������ϣ����ͼ3��ʾ��
���C�䣬A��ĺ�����ֱ�Ϊx1��x2��
��֪��ʱC��A�������������ƽ����ƽ�У�����ֱ��C��A��Ľ���ʽΪy=��x+b��
����y=x2��y=��x+b�ã�x2=��x+b����x2+x��b=0��
��x1+x2=��1��x1x2=��b��
��C��A��=1������������ã�|x1��x2|= ![]() ��
��
�ࣨx1��x2��2= ![]() ������x1+x2��2��4x1x2=
������x1+x2��2��4x1x2= ![]()
��1+4b= ![]() �����b=-
�����b=- ![]() ��
��
��x2+x+ ![]() =0�����x=
=0�����x= ![]() ��x=
��x= ![]() ��
��
�ߵ�C��ĺ�����ϴ�x= ![]() ��
��
��x= ![]() ʱ��y=x2=
ʱ��y=x2= ![]() ��
��
��P�� ![]() ��
�� ![]() ����
����
����ʱ����ת45�㣬��A��B�����������ϣ�
��Ϊ��ʱ����ת45���ֱ��A��B����y��ƽ�У���ˣ������������ֻ����һ�����㣬�ʴ������β����ڣ�
����ʱ����ת45�㣬��B��C�����������ϣ����ͼ4��ʾ��
���ͬ��������ã�P�� ![]() ��
�� ![]() ����
����
����ʱ����ת45�㣬��C��A�����������ϣ����ͼ5��ʾ��
���ͬ��������ã�P�� ![]() ��
�� ![]() ����
����
������������P����������0�� ![]() ������
������ ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ��
��
����������1������ת���ʼ�����ֱ�������α߽ǹ�ϵ��⣻��2��������ȷ��ABC��ԭ�㰴˳ʱ�뷽����ת45���������μ�Ϊ��DEF��Ȼ�����������������ۣ��ֱ������⣻��3����ת������˳ʱ�롢��ʱ�����ֿ��ܣ������������ϵĵ��е�A�͵�B����B�͵�C����C�͵�D���ֿ��ܣ���˹������ֿ��ܵ����Σ���Ҫ�������ۣ�����©�⣮
�����㾫����������Ҫ������ƽ�Ƶ����ʺ���ת�����ʵ����֪ʶ�㣬��Ҫ���բپ���ƽ��֮���ͼ����ԭ����ͼ�εĶ�Ӧ�߶�ƽ�У�����ͬһֱ���ϣ�����ȣ���Ӧ����ȣ�ͼ�ε���״���С��û�з����仯���ھ���ƽ�ƺ�Ӧ���������߶�ƽ�У�����ͬһֱ���ϣ�����ȣ�����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��˲�����ȷ�����⣮

����Ŀ��ij����ί�ٰ조�ҵ��й��Ρ�Ϊ�����֪ʶ�������ס�������ѧУ����������ȣ�������������ѧ���ɼ��ֱ�Ϊ70�֡�80�֡�90�֡�100�֣�������ͳ�����ݻ��������²�������ͳ��ͼ����

��У�ɼ�ͳ�Ʊ�
����/�� | ����/�� |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)��ͼ���У���80�֡��������ε�Բ�ĽǶ���Ϊ________��
(2)���㽫ͼ�ڲ���������
(3)����У�ɼ���ƽ���֣�
(4)������֪s��2��135��s��2��175������������������ݣ��Լס�����У�ɼ������������ۣ�