题目内容
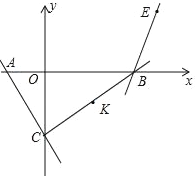
【题目】在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒 
个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒．
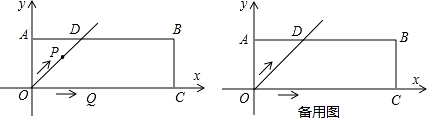
（1）当点P移动到点D时，求出此时t的值；
（2）当t为何值时，△PQB为直角三角形；
（3）已知过O、P、Q三点的抛物线解析式为y=﹣ 
（x﹣t）2+t（t＞0）．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．
【答案】
（1）
解：∵四边形OABC是矩形，
∴∠AOC=∠OAB=90°，
∵OD平分∠AOC，
∴∠AOD=∠DOQ=45°，
∴在Rt△AOD中，∠ADO=45°，
∴AO=AD=2，OD=2 
，
∴t= 
=2
（2）
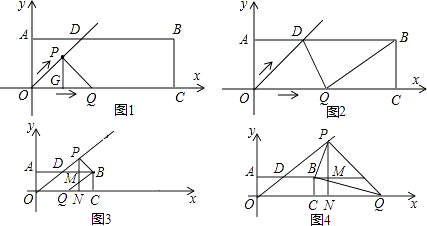
解：要使△PQB为直角三角形，显然只有∠PQB=90°或∠PBQ=90°．
如图1，作PG⊥OC于点G，在Rt△POG中，
∵∠POQ=45°，
∴∠OPG=45°，
∵OP= t，
∴OG=PG=t，
∴点P（t，t）
又∵Q（2t，0），B（6，2），
根据两点间的距离公式可得：PB2=（6﹣t）2+（2﹣t）2，QB2=（6﹣2t）2+22，PQ2=（2t﹣t）2+t2=2t2，
①若∠PQB=90°，则有PQ2+BQ2=PB2，
即：2t2+[（6﹣2t）2+22]=（6﹣t）2+（2﹣t）2，
整理得：4t2﹣8t=0，
解得：t1=0（舍去），t2=2，
∴t=2，
②若∠PBQ=90°，则有PB2+QB2=PQ2，
∴[（6﹣t）2+（2﹣t）2]+[（6﹣2t）2+22]=2t2，
整理得：t2﹣10t+20=0，
解得：t=5± 
．
∴当t=2或t=5+ 或t=5﹣ 时，△PQB为直角三角形．
解法2：①如图2，当∠PQB=90°时，
易知∠OPQ=90°，
∴BQ∥OD
∴∠BQC=∠POQ=45°
可得QC=BC=2，
∴OQ=4，
∴2t=4，
∴t=2，
②如图3，当∠PBQ=90°时，若点Q在OC上，
作PN⊥x轴于点N，交AB于点M，
则易证∠PBM=∠CBQ，
∴△PMB∽△QCB
∴ 
= 
，
∴CBPM=QCMB，
∴2（t﹣2）=（2t﹣6）（6﹣t），
化简得t2﹣10t+20=0，
解得：t=5± ，
∴t=5﹣ ；
③如图4，当∠PBQ=90°时，若点Q在OC的延长线上，
作PN⊥x轴于点N，交AB延长线于点M，
则易证∠BPM=∠MBQ=∠BQC，
∴△PMB∽△QCB，
∴ = ，
∴CBPM=QCMB，
∴2（t﹣2）=（2t﹣6）（t﹣6），
化简得t2﹣10t+20=0，
解得：t=5± ，
∴t=5+
（3）
解：存在这样的t值，理由如下：
将△PQB绕某点旋转180°，三个对应顶点恰好都落在抛物线上，
则旋转中心为PQ中点，此时四边形PBQB′为平行四边形．
∵PO=PQ，由P（t，t），Q（2t，0），知旋转中心坐标可表示为（ 
t， 
t），
∵点B坐标为（6，2），
∴点B′的坐标为（3t﹣6，t﹣2），
代入y=﹣ 
（x﹣t）2+t，得：2t2﹣13t+18=0，
解得：t1= 
，t2=2
【解析】（1）首先根据矩形的性质求出DO的长，进而得出t的值；（2）要使△PQB为直角三角形，显然只有∠PQB=90°或∠PBQ=90°，进而利用勾股定理分别分析得出PB2=（6﹣t）2+（2﹣t）2 ， QB2=（6﹣2t）2+22 ， PQ2=（2t﹣t）2+t2=2t2 ， 再分别就∠PQB=90°和∠PBQ=90°讨论，求出符合题意的t值即可；（3）存在这样的t值，若将△PQB绕某点旋转180°，三个对应顶点恰好都落在抛物线上，则旋转中心为PQ中点，此时四边形PBQB′为平行四边形，根据平行四边形的性质和对称性可求出t的值．
【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
