题目内容
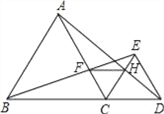
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)从图中得到AC=3,CD=2,BC=6,CE=4,∠ACB=∠DCE=90°,利用两边对应成比例且夹角相等,可证△ACB∽△DCE;
(2)由相似三角形的性质可知,∠B=∠E,可得∠B+∠A=∠E+A=90°,即∠EFA=90°,故EF⊥AB.
(1)证明:∵![]()
∴![]() =
=![]() ,
,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE;
(2)∵△ACB∽△DCE,
∴∠B=∠E,
∵∠B+∠A=90°,
∴∠E+A=90°,
即∠EFA=90°,
∴EF⊥AB.

练习册系列答案
相关题目