��Ŀ����
����Ŀ����ѧ�ڿ�ѧ����ѧУ������Ծ��꼶ij��50��ѧ��������������Ŀ�IJ��ԣ����ݲ��Գɼ���������������ͳ��ͼ�� 
����ͳ��ͼ����������⣺
��1�����β��Ե�ѧ���У���4�ֵ�ѧ���ж����ˣ�
��2�����β��Ե�ƽ�����Ƕ��ٷ֣�
��3��ͨ��һ��ʱ���ѵ����������Ըð�ѧ����������Ŀ���еڶ��β��ԣ���óɼ�����ͷ�Ϊ3�֣��ҵ�4�ֺ�5�ֵ���������45�ˣ�ƽ���ֱȵ�һ�������0.8�֣��ʵڶ��β����е�4�֡�5�ֵ�ѧ�����ж����ˣ�
���𰸡�
��1���⣺��������ã�
��4�ֵ�ѧ����50��50%=25���ˣ���
�𣺵�4�ֵ�ѧ����25��
��2���⣺��������ã�
ƽ����= ![]() =3.7���֣�
=3.7���֣�
��3���⣺��ڶ��β����е�4�ֵ�ѧ����x�ˣ���5�ֵ�ѧ����y�ˣ���������ã�
![]() ��
��
��ã� ![]() ��
��
�𣺵ڶ��β����е�4�ֵ�ѧ����15�ˣ���5�ֵ�ѧ����30��
����������1�������������Ե�4�ֵ�ѧ����ռ�İٷְټ��ɵó��𰸣���2������ƽ�����ļ��㹫ʽ�������˵ĵ÷ּ��������ٳ������������ɣ���3������ڶ��β����е�4�ֵ�ѧ����x�ˣ���5�ֵ�ѧ����y�ˣ��ٸ��ݳɼ�����ͷ�Ϊ3�֣���4�ֺ�5�ֵ���������45�ˣ�ƽ���ֱȵ�һ�������0.8�֣��г������飬���x��y��ֵ���ɣ�
�����㾫����������Ŀ����֪��������������ͳ��ͼ������ͳ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����

����Ŀ����ͼ���ڡ�ABC�У���A=120�㣬��D��BC���е㣬��E��AB�ϵ�һ�㣬��F��AC�ϵ�һ�㣬��EDF=90�㣬��BE=2��FC=7����EF= �� 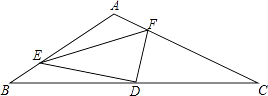
����Ŀ����ѧ��Ϊ���Ʋ����ʺ�ij������ֲ���������¶ȣ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ��ʱ����Գ�����ֲ��߶ȵ�����������������������
�¶�t/�� | ��4 | ��2 | 0 | 1 | 4 |
ֲ��߶�������l/mm | 41 | 49 | 49 | 46 | 25 |
��ѧ�Ҿ������롢�Ʋ��l��t֮���Ƕ��κ�����ϵ���ɴ˿����Ʋ����ʺ�����ֲ���������¶�Ϊ�森