Question

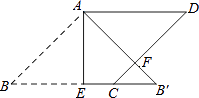
【题目】如图，矩形纸片ABCD中，AB=4，BC=8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是（ ）
A.AF=AE
B.△ABE≌△AGF
C.EF=2
D.AF=EF

Answer 1

【答案】D
【解析】解：设BE=x，则CE=BC﹣BE=8﹣x， ∵沿EF翻折后点C与点A重合，
∴AE=CE=8﹣x，
在Rt△ABE中，AB2+BE2=AE2 ，
即42+x2=（8﹣x）2
解得x=3，
∴AE=8﹣3=5，
由翻折的性质得，∠AEF=∠CEF，
∵矩形ABCD的对边AD∥BC，
∴∠AFE=∠CEF，
∴∠AEF=∠AFE，
∴AE=AF=5，
∴A正确；
在Rt△ABE和Rt△AGF中，
，
∴△ABE≌△AGF（HL），
∴B正确；
过点E作EH⊥AD于H，则四边形ABEH是矩形，
∴EH=AB=4，
AH=BE=3，
∴FH=AF﹣AH=5﹣3=2，
在Rt△EFH中，EF=2 ，
∴C正确；
∵△AEF不是等边三角形，
∴EF≠AF，
故D错误；
故选：D．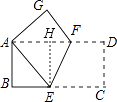

【考点精析】关于本题考查的翻折变换（折叠问题），需要了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．