题目内容
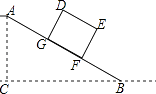
【题目】如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF= . 
【答案】![]()
【解析】解:延长ED至G,使DG=DE,连接CG、FG,如图所示: 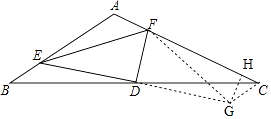
在△CDG和△BDE中,
∵  ,
,
∴△CDG≌△BDE(SAS),
∴CG=BE=2,∠GCD=∠B,
∵∠A=120°,
∴∠B+∠ACB=60°,
∴∠DCG+∠ACB=60°,即∠GCF=60°,
过点G作GH⊥FC于点H,
∴GH=GCsin∠GCF=2× ![]() =
= ![]() ,CH=GCcos∠GCF=2×
,CH=GCcos∠GCF=2× ![]() =1,
=1,
则FH=FC﹣CH=7﹣1=6,
∵DE⊥DF,DG=DE,
∴EF=FG= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
相关题目
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.