题目内容
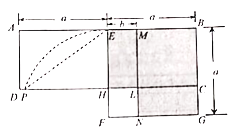
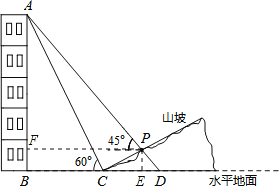
【题目】如图,某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=60m,山坡的坡比为1:2.
(1)求该建筑物的高度(即AB的长,结果保留根号);
(2)求此人所在位置点P的铅直高度(即PD的长,结果保留根号).

【答案】(1) 建筑物的高度为60![]() 米; (2)点P的铅直高度为(20
米; (2)点P的铅直高度为(20![]() ﹣20)米.
﹣20)米.
【解析】
(1)过点P作PE⊥BD于E,PF⊥AB于F,在Rt△ABC中,求出AB的长度即可;
(2)设PE=x米,则BF=PE=x米,根据山坡坡度为1:2,用x表示CE的长度,然后根据AF=PF列出等量关系式,求出x的值即可.
解:(1)过点P作PE⊥BD于E,PF⊥AB于F,
又∵AB⊥BC于B,
∴四边形BEPF是矩形,
∴PE=BF,PF=BE
∵在Rt△ABC中,BC=90米,∠ACB=60°,
∴AB=BCtan60°=60![]() (米),
(米),
故建筑物的高度为60![]() 米;
米;
(2)设PE=x米,则BF=PE=x米,
∵在Rt△PCE中,tan∠PCD=![]() ,
,
∴CE=2x,
∵在Rt△PAF中,∠APF=45°,
∴AF=AB﹣BF=60![]() ﹣x,
﹣x,
PF=BE=BC+CE=60+2x,
又∵AF=PF,
∴60﹣x=60+2x,
解得:x=20![]() ﹣20,
﹣20,
答:人所在的位置点P的铅直高度为(20![]() ﹣20)米.
﹣20)米.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目