题目内容
【题目】如图,在平面直角坐标系xOy中,等边△AOB的边长为10,点C在边OA上,点D在边AB上,且OC=3BD.反比例函数y=![]() (k≠0)的图象恰好经过C、D两点,则k的值为_____.
(k≠0)的图象恰好经过C、D两点,则k的值为_____.
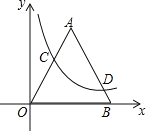
【答案】![]()
【解析】
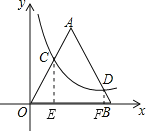
过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,设BD=a,则OC=3a,根据等边三角形的性质结合解含30度角的直角三角形,可得出点C、D的坐标,再利用反比例函数图象上点的坐标特征即可求出a、k的值,此题得解.
解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,如图所示.
设BD=a,则OC=3a.
∵△AOB为边长为10的等边三角形,
∴∠COE=∠DBF=60°,OB=10.
在Rt△COE中,∠COE=60°,∠CEO=90°,OC=3a,
∴∠OCE=30°,
∴OE=![]() ,CE=
,CE=![]() ,
,
∴点C(![]() ,
,![]() ).
).
同理,可求出点D的坐标为(![]() ,
,![]() ).
).
∵反比例函数y=![]() (k≠0)的图象经过点C和点D,
(k≠0)的图象经过点C和点D,
∴k=![]() =
=![]() ,
,
∴a=2,k=![]() .
.
故答案为![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目