题目内容
【题目】如图,在△ABC中,∠B=50°,点D为边AB的中点,点E在边AC上,将△ADE沿DE折叠,使得点A恰好落在BC的延长线上的点F处,DF与AC交于点O,连结CD,则下列结论一定正确的是( )
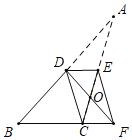
A. CE=EFB. ∠BDF=90°
C. △EOD和△COF的面积相等D. ∠BDC=∠CEF+∠A
【答案】A
【解析】
由折叠的性质和等腰三角形的判定得出选项A正确;由等腰三角形的性质和三角形内角和定理得出选项B不正确;由DE∥BC判断选项C不正确;由三角形的外角性质判断选项D不正确.
解:∵点D为边AB的中点,
∴AD=BD,由折叠知,FD=AD,∠DFE=∠A,
∴BD=FD,
∴∠B=∠DFB,
∵∠EFC=∠DFB+∠DFE,∠ECF=∠B+∠A,
∴∠EFC=∠ECF,
∴CE=EF,故A正确;
∵BD=FD,
∴∠B=∠DFB=50°,
∴∠BDF=180°﹣2×50°=80°,故B不正确;
由折叠知,EF=AE,
∴AE=CE,
∵BD=CD,
∴DE是△ABC的中位线,
∴DE∥BC,AB=2DE,
∴△DCE的面积=△DEF的面积,△CFD的面积=△CFE的面积,
当DE=CF时,△EOD和△COF的面积相等,故C不正确;
∵∠BDC=∠DCE+∠A,
当CD∥EF时,∠DCE=∠CEF,∠BDC=∠CEF+∠A,
故D不正确;
故选:A.

练习册系列答案
相关题目