题目内容
【题目】如图,在△ABC中,BC=10,BC边上的高为3.将点A绕点B逆时针旋转90°得到点E,绕点C顺时针旋转90°得到点D.沿BC翻折得到点F,从而得到一个凸五边形BFCDE,求五边形BFCDE的面积.

【答案】80
【解析】
将点C绕点B逆时针旋转90°得到点G,绕点C顺时针旋转90°得到点H,连接EG、DH、GH,则△EBG≌△ABC≌△HDC,四边形BCHG是正方形,六边形BCDHGE是中心对称图形,根据轴对称和中心对称的性质得出S△BEG=S△CDH=S△ABC,S四边形BCDE=![]() S六边形BCDHGE,然后由S五边形BFCDE=S四边形BCDE+S△BFC即可求得.
S六边形BCDHGE,然后由S五边形BFCDE=S四边形BCDE+S△BFC即可求得.
将点C绕点B逆时针旋转90°得到点G,绕点C顺时针旋转90°得到点H,连接EG、DH、GH,则△EBG≌△ABC≌△HDC,四边形BCHG是正方形,六边形BCDHGE是中心对称图形,
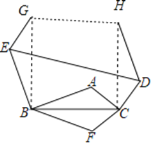
∴四边形BCDE≌四边形HGED,
∵S△BEG=S△CDH=S△ABC=![]() ×10×3=15=S△BFC,S正方形BCHG=10×10=100,
×10×3=15=S△BFC,S正方形BCHG=10×10=100,
∴S六边形BCDHGE=S△BEG+S△CDH+S正方形BCHG=2×15+100=130,
∴S四边形BCDE=![]() S六边形BCDHGE=65,
S六边形BCDHGE=65,
∴S五边形BFCDE=S四边形BCDE+S△BFC=65+15=80,
故答案为:80.

练习册系列答案
相关题目