题目内容
【题目】已知,在平面直角坐标系中,点![]() ,
,![]() ,过
,过![]() 点作直线
点作直线![]() 与
与![]() 轴互相垂直,
轴互相垂直,![]() 为
为![]() 轴上的一个动点,且
轴上的一个动点,且![]() .
.
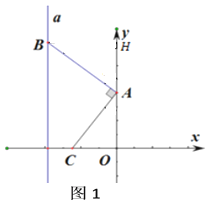
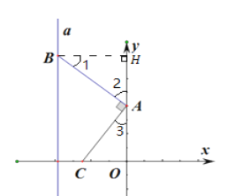
(1)如图1,若点![]() 是第二象限内的一个点,且
是第二象限内的一个点,且![]() 时,求点
时,求点![]() 的坐标;(用
的坐标;(用![]() 的代数式表示)
的代数式表示)
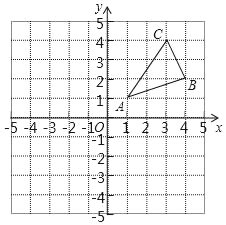
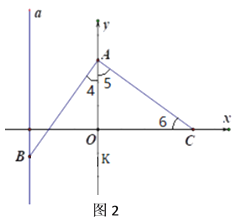
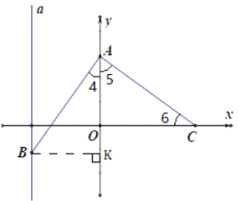
(2)如图2,若点![]() 是第三象限内的一个点,设
是第三象限内的一个点,设![]() 点的坐标
点的坐标![]() ,求
,求![]() 的取值范围:
的取值范围:
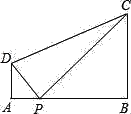
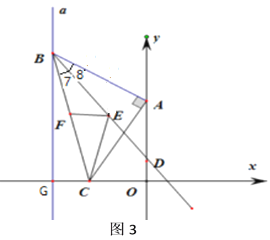
(3)如图3,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,点
,点![]() 、
、![]() 分别是射线
分别是射线![]() 与边
与边![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() ,当
,当![]() 时,试求
时,试求![]() 的最小值.
的最小值.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过![]() 点作
点作![]() 轴于点
轴于点![]() ,由
,由![]() ,即可得出点C的坐标;
,即可得出点C的坐标;
(2)过![]() 点作
点作![]() 轴于点
轴于点![]() ,由
,由![]() ,得到点C的坐标,再由点C在在
,得到点C的坐标,再由点C在在![]() 轴负半轴,得出结果即可;
轴负半轴,得出结果即可;
(3)在![]() 上取点
上取点![]() ,使
,使![]() ,得出
,得出![]() ,进而得出当
,进而得出当![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]() 与
与![]() 重合时候,
重合时候,![]() 取到最小值,即
取到最小值,即![]() ,再利用
,再利用![]() =
=![]() 得到关于AC的方程,求解即可.
得到关于AC的方程,求解即可.
解:(1)如图,过![]() 点作
点作![]() 轴于点
轴于点![]() ,
,
则![]() ,
,![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,点
,点![]() 在
在![]() 轴负半轴
轴负半轴
![]() 点
点![]() 的坐标为
的坐标为![]()
(2)如图,过![]() 点作
点作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 点的坐标
点的坐标![]()
![]()
![]()
![]() 点
点![]() 是第三象限内的一个点
是第三象限内的一个点
![]()
![]() 即
即![]() .
.
(3)如图,在![]() 上取点
上取点![]() ,使
,使![]()
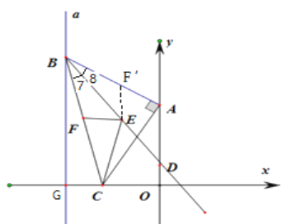
![]() 是
是![]() 的平分线
的平分线
![]()
![]()
![]()
![]()
![]()
当![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]() 与
与![]() 重合时候,
重合时候,
![]() 取到最小值,此时
取到最小值,此时![]()
由(1)知,点![]() 的坐标为
的坐标为![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() 的最小值为
的最小值为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某科研小组获取了声音在空气中传播的速度v与空气温度t关系的一些数据如下表:
温度t(°C) | -20 | -10 | 0 | 10 | 20 | 30 |
声速v(m/s) | 318 | 324 | 330 | 336 | 342 | 348 |
(1)根据表中提供的信息,可推测速度v是温度t的一次函数,请你写出其函数表达式;
(2)当空气温度为25°C,声音10秒可以传播多少米?