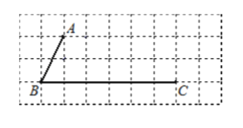题目内容
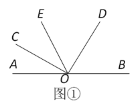
【题目】操作与探究:已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.
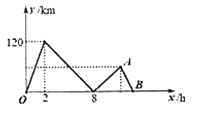
(1)如图①所示,若∠COE=20°,则∠BOD= °.
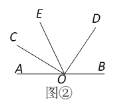
(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;
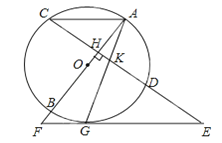
(3)若将∠COD绕点O旋转至图③的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系: .

【答案】(1)40°;(2)∠BOD=2∠COE,理由见详解;(3)∠BOD+2∠COE=360°,理由见详解
【解析】
(1)由互余得∠DOE的度数,进而由角平分线得出∠AOE的度数,即可得出∠BOD的度数;
(2)由互余及角平分线得∠DOE=90°-∠COE=∠AOE,∠AOC=∠AOE-∠COE=90°-2∠COE,最后根据∠BOD=180°-∠AOC-∠COD可得;
(3)由互余得∠DOE=∠COE-90°,由角平分线得∠AOD=2∠DOE=2∠COE-180°,最后根据∠BOD=180°-∠AOD可得.
解:(1)![]()
∵射线OE平分∠AOD
∴![]()
∴![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵∠COD=90°
∴∠DOE=∠COE-90°
∵射线OE平分∠AOD
∴∠AOC=∠AOE-∠COE=90°-2∠COE
∵A,O,B在同一直线上
∴∠BOD=180°-∠AOC-∠COD=180°-(90°-2∠COE)- 90°
即:∠BOD=2∠COE;
(3)∠BOD+2∠COE=360°,理由如下:
∵∠COD=90°
∴∠DOE=∠COE-90°
∵射线OE平分∠AOD
∴∠AOD=2∠DOE=2∠COE-180°
∴∠BOD=180°-∠AOD=360°-2∠COE
即:∠BOD+2∠COE=360°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目