题目内容
【题目】如图所示,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=![]() R.其中能使得BC=R的有________(填序号).
R.其中能使得BC=R的有________(填序号).
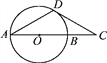
【答案】①②③④
【解析】首先连接OD,由CD是⊙O的切线,可得OD⊥CD,然后由①AD=CD;②∠A=30°;③∠ADC=120°;可求得∠C的度数,即可得OC=2OD=2R,继而求得BC的长,又由④DC=![]() R,即可求得OC的长,继而求得BC=R.
R,即可求得OC的长,继而求得BC=R.
连接OD,
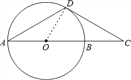
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
①∵AD=CD,
∴∠A=∠C,
∵∠COD=2∠A,
∴∠C=30°,
∴OC=2OD,
∵OD=OB,
∴BC=OB=R;
②∵∠A=30°,
∴∠COD=2∠A=60,
∴∠C=30°,
∴OC=2OD,
∵OD=OB,
∴BC=OB=R;
③∵∠ADC=120°,
∴∠ODA=30°,
∵OA=OD,
∴∠A=30°,
∴∴∠COD=2∠A=60°,
∴∠C=30°,
∴OC=2OD,
∵OD=OB,
∴BC=OB=R;
④∵DC=![]() R,
R,
∴OC=![]() =2R,
=2R,
∴BC=OCOB=R.
故答案为:①②③④

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目