题目内容
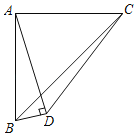
【题目】如图,等腰直角三角形ABC的直角边的长是a,AD⊥BD,且AD=3BD,则△BCD的面积是_____.
【答案】![]() a2.
a2.
【解析】
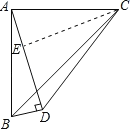
作CE⊥AD于E点,根据等腰直角三角形的性质得到∠BAC=90°,AB=AC,利用等角的余角相等得∠BAD=∠ACE,又AB=CA,∠ADB=∠AEC=90°,根据全等三角形的判定得到△ABD≌△CAE,利用全等三角形的性质有BD=AE,AD=CE,又AD=3BD,BD=x,则AD=CE=3x,根据勾股定理可计算出AB![]() x,得到x
x,得到x![]() a,根据S△CBD=S△ABD+S△ADC﹣S△ABC计算即可.
a,根据S△CBD=S△ABD+S△ADC﹣S△ABC计算即可.
作CE⊥AD于E点,∴∠AEC=90°,
∴∠ACE+∠EAC=90°.
∵△ABC是等腰直角三角形,
∴∠BAC=90°,AB=AC,
∴∠BAD+∠DAC=90°,
∴∠BAD=∠ACE.
在△ABD和△CAE中,
∵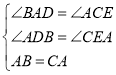 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
设BD=x,则AD=CE=3x,
由勾股定理得:AB![]() x,即
x,即![]() x=a,
x=a,
解得:x![]() a,
a,
则S△CBD=S△ABD+S△ADC﹣S△ABC
![]() a
a![]() a
a![]() a
a![]() a
a![]() a2
a2
![]() a2.
a2.
故答案为:![]() a2.
a2.

练习册系列答案
相关题目