题目内容
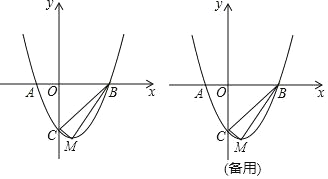
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为![]() 、
、![]() 、
、![]() ,若AD=2,AB=
,若AD=2,AB=![]() ,∠A=60°,则
,∠A=60°,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
【答案】A
【解析】
由特殊角的三角函数计算出平行四边形AB边上的高DH,从而得出平行四边形ABCD的面积,进而得出S△PBC、S2+S3的值,由E、F分别是PB、PC(靠近点P)的三等分点以及∠FPE=∠CPB可得△PEF∽△PBC,根据相似三角形的性质得出△PEF与△PBC的面积之比,从而得出S1的值,最后求出S1+ S2+ S3的值即可.
作DH⊥AB交AB于点H,
∵AD=2,AB=2![]() ,∠A=60°,
,∠A=60°,
∴DH=AD·sin60°=2×![]() =
=![]() ,
,
∴S平行四边形ABCD=2![]() ×
×![]() =6,
=6,
∴S△PBC=S2+S3=3,
∵E、F分别是PB、PC的三等分点,
∴![]() =
=![]() =
=![]() ,
,
∵∠FPE=∠CPB,
∴△PEF∽△PBC,
∴![]() =
=![]() ,
,
∴S1=![]() ,
,
∴S1+ S2+ S3=![]() +3=
+3=![]() .
.

故选A.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目