题目内容
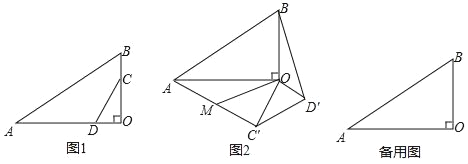
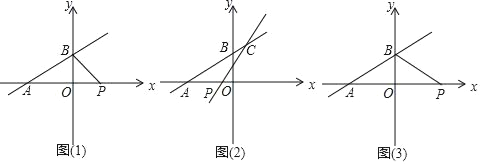
【题目】如图1,一次函数y=![]() x+4与x轴、y轴分别交于A,B两点.P是x轴上的动点,设点P的横坐标为n.
x+4与x轴、y轴分别交于A,B两点.P是x轴上的动点,设点P的横坐标为n.
(1)当△BPO∽△ABO时,求点P的坐标;
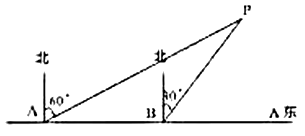
(2)如图2,过点P的直线y=2x+b与直线AB相交于C,求当△PAC的面积为20时,点P的坐标;
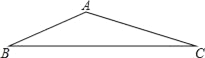
(3)如图3,直接写出当以A,B,P为顶点的三角形为等腰三角形时,点P的坐标.
【答案】(1)P(﹣2,0)或(2,0);(2)P(﹣4+2![]() ,0)或(﹣4﹣2
,0)或(﹣4﹣2![]() ,0);(3)点P的坐标为(﹣8+4
,0);(3)点P的坐标为(﹣8+4![]() ,0)或(﹣8﹣4
,0)或(﹣8﹣4![]() ,0)或(8,0)或(﹣3,0).
,0)或(8,0)或(﹣3,0).
【解析】
(1)根据坐标轴上点的特点求出A,B坐标,进而求出OA,OB,最后用相似三角形得出比例式建立方程即可得出结论;
(2)先求出点C坐标,点P坐标,利用三角形的面积公式建立方程求解即可得出结论;
(3)先求出AB2=80,AP2=(n+8)2,BP2=n2+16,利用等腰三角形分三种情况建立方程求解即可得出结论.
解:(1)一次函数y=![]() x+4,
x+4,
令x=0,
∴y=4,
∴B(0,4),
∴OB=4,
令y=0,
∴0=![]() x+4,
x+4,
∴x=﹣8,
∴A(﹣8,0),
∴OA=8,
∵△BPO∽△ABO,
∴![]() ,
,
∴OP=![]() =2,
=2,
∴n=±2,
∴P(﹣2,0)或(2,0);
(2)直线y=2x+b①与直线AB:y=![]() x+4②相交于C,
x+4②相交于C,
联立①②解得,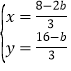 ,
,
针对于直线PC:y=2x+b,令y=0,
∴2x+b=0,
∴x=﹣![]() b,
b,
∵△PAC的面积为20,
∴S△PAC=![]() |﹣
|﹣![]() b﹣(﹣8)|×|
b﹣(﹣8)|×|![]() |=20,
|=20,
∴b=16±4![]() ,
,
∴n=﹣![]() (16±4
(16±4![]() )=﹣4±2
)=﹣4±2![]() ,
,
∴P(﹣4+2![]() ,0)或(﹣4﹣2
,0)或(﹣4﹣2![]() ,0);
,0);
(3)由(1)知,A(﹣8,0),B(0,4),
∵P(n,0),
∴AB2=80,AP2=(n+8)2,BP2=n2+16,
∵以A,B,P为顶点的三角形为等腰三角形,
∴①当AB=AP时,
∴AB2=AP2,
∴80=(n+8)2,
∴n=﹣8±4![]() ,
,
∴P(﹣8+4![]() ,0)或(﹣8﹣4
,0)或(﹣8﹣4![]() ,0),
,0),
②当AB=BP时,
∴AB2=BP2,80=n2+16,
∴n=8或n=﹣8(和点A重合,所以,舍去),
∴P(8,0),
③当AP=BP时,
∴AP2=BP2,(n+8)2=n2+16,
∴n=﹣3,
∴P(﹣3,0),
即:点P的坐标为(﹣8+4![]() ,0)或(﹣8﹣4
,0)或(﹣8﹣4![]() ,0)或(8,0)或(﹣3,0).
,0)或(8,0)或(﹣3,0).