题目内容
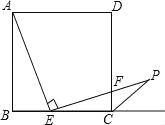
【题目】如图,在正方形ABCD中,AB=2cm,对角线AC、BD交于点O,点E以一定的速度从A向B移动,点F以相同的速度从B向C移动,连结OE、OF、EF.则线段EF的最小值是_______cm.

【答案】![]()
【解析】根据正方形的对角线互相平分且相等可得AO=BO,∠AOB=90°,对角线平分一组对角可得∠OAE=∠OBF,再根据AE=BF,然后利用“SAS”证明△AOE和△BOF全等,根据全等三角形对应角相等可得∠AOE=∠BOF,可得∠EOF=90°,然后利用勾股定理列式计算即可得解.
解:(1)在正方形ABCD中,AO=BO,∠AOB=90°,∠OAE=∠OBF=45°,
∵点E、F的速度相等,
∴AE=BF,
在△AOE和△BOF中,
OA=BO,∠AOE=∠OBF,AE=BF,
∴△AOE≌△BOF(SAS),
故答案为BOF.
(2)∵△AOE≌△BOF,
∴∠AOE=∠BOF,
∴∠AOE+∠BOE=90°,
∴∠BOF+∠BOE=90°,
∴∠EOF=90°,
在Rt△BEF中,设AE=x,则BF=x,BE=2﹣x,
EF=![]() =
=![]() =
=![]() .
.
∴当x=1时,EF有最小值为![]()
![]() ;
;
故答案为![]()
![]() .
.
“点睛”本题考查了正方形的性质,全等三角形的判定与性质,同角的余角相等的性质,熟记正方形的性质,求出三角形全等的条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:
选手 | 甲 | 乙 | 丙 |
平均数 | 9.3 | 9.3 | 9.3 |
方差 | 0.026 | a | 0.032 |
已知乙是成绩最稳定的选手,且乙的10次射击成绩不都一样,则a的值可能是( )
A. 0B. 0.020C. 0.030D. 0.035