��Ŀ����
 ��֪������a��b�Ľ���ʽ�ֱ��ǹ���y��x�Ĺ�ϵʽ��y=x2-2mx-
��֪������a��b�Ľ���ʽ�ֱ��ǹ���y��x�Ĺ�ϵʽ��y=x2-2mx-| m2 |
| 2 |
| m2+2 |
| 2 |
��1������2�ֲ�ͬ�ķ������ж�������a��b������������E������������F��
��2����m����ij��ʱ���������������У�ֻ��һ����x�ύ��A��B��A������������ͬ�ĵ㣬�������������߾���A��B���㣿Ϊʲô�������A��B��������ꣻ
��3����m=1ʱ��ֱ��x=n���������ߵĶԳ���֮��ƽ���ƶ������ҷֱ����������߽���C��D���㣬���߶�CD�ij�Ϊw����ô��д��w��n֮��ĺ�����ϵ�����ʵ�nΪʲôֵʱw������ֵ�Ƕ��٣�
���㣺���κ����ۺ���
ר�⣺ѹ����
��������1������һ�����ݶ�����ϵ�����������ȷ���������ߵĿ��ڷ��Ӷ������жϣ�
�����������ݷǸ���������ȷ��������������������ȷ������������y��Ľ��㣬�Ӷ������жϣ�
��2�����ݳ������֪������b������mȡ��ֵ������y���������ཻ���Ӷ�ȷ������x��ʼ����������ͬ�Ľ��㣬��������a��m=0ʱ��x��ֻ��һ�����㣬Ȼ����m=0��⼴�ɵõ���A��B�����ꣻ
��3���������������Ľ���ʽ��ʾ��CD���ٸ��ݶ��κ�������ֵ������
�����������ݷǸ���������ȷ��������������������ȷ������������y��Ľ��㣬�Ӷ������жϣ�
��2�����ݳ������֪������b������mȡ��ֵ������y���������ཻ���Ӷ�ȷ������x��ʼ����������ͬ�Ľ��㣬��������a��m=0ʱ��x��ֻ��һ�����㣬Ȼ����m=0��⼴�ɵõ���A��B�����ꣻ
��3���������������Ľ���ʽ��ʾ��CD���ٸ��ݶ��κ�������ֵ������
����⣺��1������һ����������a������ϵ��1��0��
�������߿������ϣ�
��������b������ϵ��-1��0��
�������߿������£�
��������b������E��������a������F��
��������m��0ʱ��
��������a�ij�����-
��0��
��������a��y��ĸ������ཻ��
��������b�ij�����
��0��
��������b��y����������ཻ��
���������b������E��������a������F��
��2����
=
+1��1��
��������b��y���������ཻ��
�֡�-1��0��
��������b����mȡ��ֵ����x��ʼ�����������㣬
��m=0ʱ��������aΪy=x2����x��ֻ��һ������Ϊ����ԭ��O��
��������b����A��B���㣬
m=0ʱ��������bΪy=-x2+1��
��y=0����-x2+1=0��
���x1=-1��x2=1��
��A������
��A��-1��0����B��1��0����
��3����m=1ʱ��������a��b�ֱ�Ϊy=x2-2x-
��y=-x2-2x+
��
���������ߵĶԳ���ֱ�Ϊֱ��x=-
=1��
ֱ��x=-
=-1��
��ֱ��x=n���������ߵĶԳ���֮��ƽ���ƶ���
��w=CD=��-n2-2n+
��-��n2-2n-
��=-n2-2n+
-n2+2n+
=-2n2+2��
��w=-2n2+2��
�൱n=0ʱ��w������ֵ��2��
�������߿������ϣ�
��������b������ϵ��-1��0��
�������߿������£�
��������b������E��������a������F��
��������m��0ʱ��
��������a�ij�����-
| m2 |
| 2 |
��������a��y��ĸ������ཻ��
��������b�ij�����
| m2+2 |
| 2 |
��������b��y����������ཻ��
���������b������E��������a������F��
��2����
| m2+2 |
| 2 |
| m2 |
| 2 |
��������b��y���������ཻ��
�֡�-1��0��
��������b����mȡ��ֵ����x��ʼ�����������㣬
��m=0ʱ��������aΪy=x2����x��ֻ��һ������Ϊ����ԭ��O��
��������b����A��B���㣬
m=0ʱ��������bΪy=-x2+1��
��y=0����-x2+1=0��
���x1=-1��x2=1��
��A������
��A��-1��0����B��1��0����
��3����m=1ʱ��������a��b�ֱ�Ϊy=x2-2x-
| 1 |
| 2 |
| 3 |
| 2 |
���������ߵĶԳ���ֱ�Ϊֱ��x=-
| -2 |
| 2��1 |
ֱ��x=-
| -2 |
| 2��(-1) |
��ֱ��x=n���������ߵĶԳ���֮��ƽ���ƶ���
��w=CD=��-n2-2n+
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
��w=-2n2+2��
�൱n=0ʱ��w������ֵ��2��
�����������Ƕ��κ����ۺ����ͣ���Ҫ�����˶��κ����Ŀ��ڷ����κ�����y��Ľ������꣬��������x��Ľ����������⣬�Լ����κ�������ֵ���⣬�ۺ��⣬���ѶȲ�����Ƕ��κ����������Լ���ֵ�����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����һ������ǡ�÷ֳ����������Σ����������������εı߳���ȣ������С�������εı߳�Ϊ3���ף�����������ε������
��ͼ����һ������ǡ�÷ֳ����������Σ����������������εı߳���ȣ������С�������εı߳�Ϊ3���ף�����������ε������ ��ͼ��ֱ��l��m��������45��ǵ����ǰ�ABC��ֱ�Ƕ���C����ֱ��m�ϣ���
��ͼ��ֱ��l��m��������45��ǵ����ǰ�ABC��ֱ�Ƕ���C����ֱ��m�ϣ��� ��ͼ����֪AD��BE��CF���������ν�ֱ��l1��l2�ڵ�A��B��C�͵�D��E��F�����DE��EF=3��5��AC=24����BC=
��ͼ����֪AD��BE��CF���������ν�ֱ��l1��l2�ڵ�A��B��C�͵�D��E��F�����DE��EF=3��5��AC=24����BC=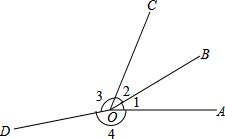 ��ͼ��OBƽ�֡�AOC���ҡ�2����3����4=1��3��4�����1����2����3����4��
��ͼ��OBƽ�֡�AOC���ҡ�2����3����4=1��3��4�����1����2����3����4��