题目内容
如图,在平面直角坐标系中,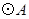 与
与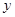 轴相切于原点
轴相切于原点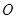 ,平行于
,平行于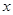 轴的直线交
轴的直线交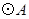 于
于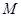 、
、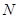 两点,若点
两点,若点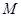 的坐标是
的坐标是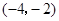 ,则弦M
,则弦M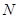 的长为 .
的长为 .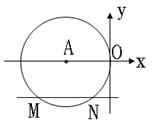
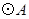 与
与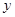 轴相切于原点
轴相切于原点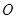 ,平行于
,平行于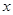 轴的直线交
轴的直线交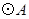 于
于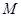 、
、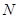 两点,若点
两点,若点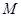 的坐标是
的坐标是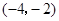 ,则弦M
,则弦M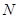 的长为 .
的长为 .
3
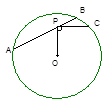
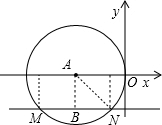
分别过点M、N作x轴的垂线,过点A作AB⊥MN,连接AN
设⊙A的半径为r.则AN=OA=r,AB=2,∵AB⊥MN,∴BM=BN,∴BN=4-r;
则在Rt△ABN中,根据勾股定理,得AB2+BN2=AN2,即:22+(4-r)2=r2,解得r=2.5,
则N到y轴的距离为1,又∵点N在第三象限,∴N的坐标为(-1,-2);∴MN=3;
设⊙A的半径为r.则AN=OA=r,AB=2,∵AB⊥MN,∴BM=BN,∴BN=4-r;
则在Rt△ABN中,根据勾股定理,得AB2+BN2=AN2,即:22+(4-r)2=r2,解得r=2.5,
则N到y轴的距离为1,又∵点N在第三象限,∴N的坐标为(-1,-2);∴MN=3;


练习册系列答案
相关题目
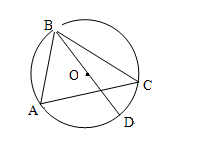
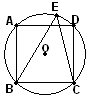
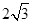 ,0C=1,则半径OB的长为________.
,0C=1,则半径OB的长为________.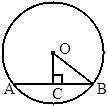
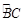 上一点,若
上一点,若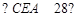 ,则
,则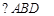 ___________度.
___________度.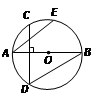
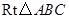 中,
中,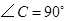 ,
,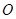 为直角边
为直角边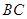 上一点,以
上一点,以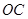 为半径的圆恰好与斜边
为半径的圆恰好与斜边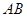 相切于点
相切于点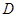 ,与
,与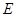 .
.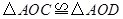
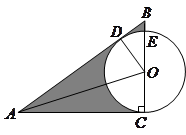
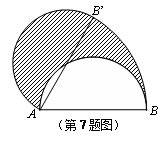
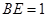 ,
,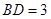 ,求圆O的半径及图中阴影部分的面积
,求圆O的半径及图中阴影部分的面积 .
.
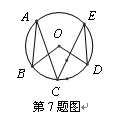
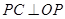 ,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .
,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .