题目内容
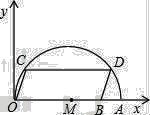
【题目】如图所示,小明家小区空地上有两棵笔直的树![]() 、
、![]() .一天,他在
.一天,他在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,在
,在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,线段
,线段![]() 恰好经过树顶
恰好经过树顶![]() .已知
.已知![]() 、
、![]() 两处的距离为
两处的距离为![]() 米,两棵树之间的距离
米,两棵树之间的距离![]() 米,
米,![]() 、
、![]() 、
、![]() 、
、![]() 四点.在一条直线上,求树
四点.在一条直线上,求树![]() 的高度.(结果精确到
的高度.(结果精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() ,
,![]() .)
.)

【答案】树![]() 的高度约为
的高度约为![]() 米.
米.
【解析】
设CD=xm,先在Rt△BCD中,由于∠DBC=45°,则根据等腰直角三角形的性质得BC=CD=x,再在Rt△DAC中,利用正切定义得到x=0.62(x+2),解得![]() ,即
,即![]() 然后在Rt△FBE中根据等腰直角三角形的性质FE=BE=BC+CE≈6.3.
然后在Rt△FBE中根据等腰直角三角形的性质FE=BE=BC+CE≈6.3.
设CD=xm,
在Rt△BCD中,
∵![]()
∴BC=CD=x,
在Rt△DAC中,∵![]()
∴![]()
∴![]()
∴x=0.62(x+2),
解得![]() ,
,
∴![]()
在Rt△FBE中,
∵![]()
∴FE=BE=BC+CE=6219+3≈6.3.
答:树EF的高度约为6.3米.

练习册系列答案
相关题目