题目内容
【题目】如果二次函数y=x2+(k+2)x+k+5的图象与x轴的两个不同交点的横坐标都是正的,那么k值应为( )
A. k>4或k<﹣5 B. ﹣5<k<﹣4 C. k≥﹣4或k≤﹣5 D. ﹣5≤k≤﹣4
【答案】B
【解析】
先令x2+(k+2)x+k+5=0,再设函数图象与x轴两交点的坐标分别为(x1,0)(x2,0),根据根与系数的关系及根的判别式得到关于k的不等式组,求出k的取值范围即可.
令x2+(k+2)x+k+5=0,设函数图象与x轴两交点的坐标分别为(x1,0)(x2,0),
∵函数图象与x轴两交点的坐标都是正的,且x1≠x2,
∴x1+x2=-(k+2)>0,x1x2=k+5>0,△=(k+2)2-4(k+5)>0,
即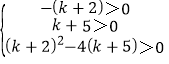 ,
,
解得-5<k<-4.
故选B.

练习册系列答案
相关题目
【题目】甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
应聘者 | 笔试 | 口试 | 得票 |
甲 | 85 | 83 | 90 |
乙 | 80 | 85 | 92 |
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?