题目内容
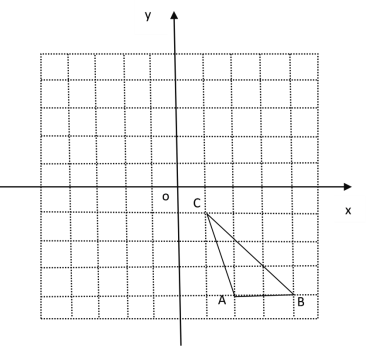
【题目】如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
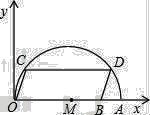
【答案】(2,6)
【解析】
过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.
∵四边形OCDB是平行四边形,点B的坐标为(16,0),
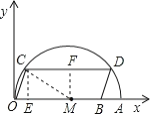
CD∥OA,CD=OB=16,
过点M作MF⊥CD于F,则![]()
过C作CE⊥OA于E,
∵A(20,0),
∴OA=20,OM=10,
∴OE=OMME=OMCF=108=2,
连接MC,![]()
∴在Rt△CMF中,
![]()
∴点C的坐标为(2,6).
故答案为:(2,6).

练习册系列答案
相关题目
【题目】现在要从甲、乙两名学生中选择一名学生去参加比赛,因甲乙两人的5次测试总成绩相同,所以根据他们的成绩绘制了尚不完整的统计图表进行分析.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 90 | 70 | 80 | 100 | 60 |
乙成绩 | 70 | 90 | 90 | a | 70 |
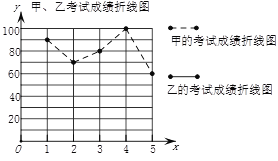
请同学们完成下列问题:
(1)a=________,![]() =________;
=________;
(2)请在图中完成表示乙成绩变化情况的折线:
(3)S2甲=200,请你计算乙的方差;
(4)可看出________将被选中参加比赛.(第1问和第4问答案可直接填写在答题卡的横线上)