题目内容
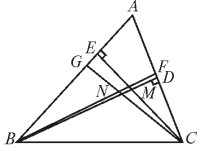
锐角△ABC中，BD和CE是两条高，相交于点M，BF和CG是两条角平分线，相交于点N，如果∠BMC=100°，求∠BNC的度数．
130°
∵BD、CE是△ABC的高
∴∠BDC=∠CEB=90°
∴∠ABC=90°－∠BCE
∠ACB=90°－∠CBD
又∵∠BMC=100°
∴∠DBC+∠BCE=80°
∴∠ABC+∠ACB=100°
∵BF、CG是△ABC的角平分线．
∴∠BCG=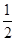
∠ACB，∠CBF=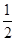∠ABC
∴∠BNC=180°－（∠BCG+∠CBF）
=180°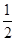－（∠ABC+∠ACB）
=130°
∴∠BDC=∠CEB=90°
∴∠ABC=90°－∠BCE
∠ACB=90°－∠CBD
又∵∠BMC=100°
∴∠DBC+∠BCE=80°
∴∠ABC+∠ACB=100°
∵BF、CG是△ABC的角平分线．
∴∠BCG=
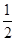∠ACB，∠CBF=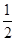∠ABC∴∠BNC=180°－（∠BCG+∠CBF）
=180°－
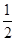（∠ABC+∠ACB）=130°
练习册系列答案
相关题目
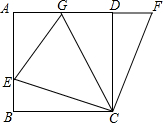
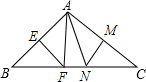
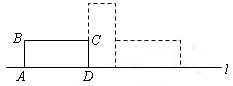
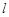上进行两次旋转，则点B在两次旋转过程中经过的路径的长是（ ）
