题目内容
【题目】已知,△ABC是等边三角形,四边形ACFE是平行四边形,AE=BC.
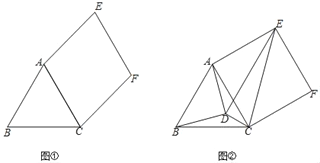
(1)如图①,求证:ACFE是菱形;
(2)如图②,点D是△ABC内一点,且∠ADB=90°,∠EDC=90°,∠ABD=∠ACE.求证:ACFE是正方形.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)由题意直接可证
(2)由题意可证△ABD≌△AGC 可证AG=AD,∠BAD=∠CAG可得△ADG是等边三角形,且根据直角三角形斜边上中线等于斜边一半,可得DG=EG=CG=AG. 即可证得结论.
证明:(1)∵△ABC是等边三角形,
∴AC=BC.
∵AE=BC,
∴AC=AE.
∵四边形ACFE是平行四边形,
∴ACFE是菱形.
(2)证明:连接AF交CE于点G,连接DG
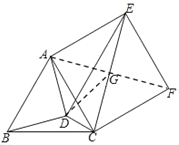
由(1)得ACFE是菱形,
∴∠AGC=90°,∠GAC=∠EAG,CG=EG.AG=GF
∵∠ADB=90°,
∴∠ADB=∠AGC.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
在△ABD和△ACG中,
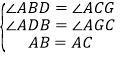
∴△ABD≌△ACG.
∴AD=AG,∠BAD=∠CAG.
∴∠BAD+∠DAC=∠CAG+∠DAC.
即∠BAC=∠DAG.
∵∠BAC=60°,
∴∠DAG=60°.
∵AD=AG,
∴△DAG是等边三角形.
∴AG=DG.
∵∠EDC=90°,CG=EG,
在Rt△EDC中,
有![]() .
.
∵AG=DG,
∴AG=CG.
∴AF=CE
又∵ACFE是菱形,
∴ACFE是正方形.

练习册系列答案
相关题目