题目内容
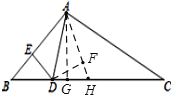
【题目】如图,点D在边BC上,∠C+∠BAD=∠DAC,过D作DE⊥AB于E,![]() ,则线段AC的长为_____.
,则线段AC的长为_____.

【答案】![]()
【解析】
如图,作∠DAH=∠DAE,交BC于H,过点D作DF⊥AH于F,过点A作AG⊥BC于G,根据角平分线的性质可得DE=DF,AE=AF,由∠C+∠BAD=∠DAC可得∠HAC=∠C,即可证明AH=CH,设DE=4x,根据![]() ,利用勾股定理可求出DF、AF的长,设FH=y,在Rt△DFH中,利用勾股定理列方程可求出y值,即可求出DH的长,利用面积法可求出AG的长,利用勾股定理可求出DG的长,即可求出CG的长,利用勾股定理求出AC的长即可得答案.
,利用勾股定理可求出DF、AF的长,设FH=y,在Rt△DFH中,利用勾股定理列方程可求出y值,即可求出DH的长,利用面积法可求出AG的长,利用勾股定理可求出DG的长,即可求出CG的长,利用勾股定理求出AC的长即可得答案.
如图,作∠DAH=∠DAE,交BC于H,过点D作DF⊥AH于F,过点A作AG⊥BC于G,
∵DE⊥AB,
∴DE=DH,AE=AF,
设DE=4x,
∵![]() ,
,
∴AE=7x,
∵AD=![]() ,AE2+AE2=AD2,
,AE2+AE2=AD2,
∴(4x)2+(7x)2=65,
解得:x=1,(负值舍去)
∴DE=4,AE=7,
∴DF=DE=4,DF=AE=7,
∵∠C+∠BAD=∠DAC,∠DAC=∠DAH+∠HAC,
∴∠HAC=∠C,
∴AH=CH,
设FH=y,
∴CH=AH=AF+FH=7+y,
∵CD=13,
∴DH=CD-CH=6-y,
在Rt△DFH中,DF2+FH2=DH2,即42+y2=(6-y)2,
解得:y=![]() ,
,
∴DH=6-![]() =
=![]() ,CH=AH=7+
,CH=AH=7+![]() =
=![]() ,
,
∴S△ADH=![]() DH·AG=
DH·AG=![]() AH·DF,即
AH·DF,即![]() ·AG=
·AG=![]() ×4,
×4,
解得:AG=8,
∴DG=![]() =1,
=1,
∴CG=CD-DG=12,
∴AC=![]() =
=![]() .
.
故答案为:![]()

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目