ЬтФПФкШн
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃН2x2+4x+kЉ1ЃЎ
ЃЈ1ЃЉЕБЖўДЮКЏЪ§ЕФЭМЯѓгыxжсгаНЛЕуЪБЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєAЃЈx1ЃЌ0ЃЉгыBЃЈx2ЃЌ0ЃЉЪЧЖўДЮКЏЪ§ЭМЯѓЩЯЕФСНИіЕуЃЌЧвЕБxЃНx1+x2ЪБЃЌyЃНЉ6ЃЌЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЌВЂдкЫљЬсЙЉЕФзјБъЯЕжаЛГіДѓжТЭМЯѓЃЛ
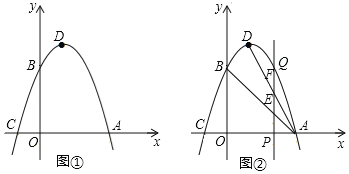
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЗелЃЌЭМЯѓЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓЃЌЕБжБЯпyЃН![]() x+mЃЈmЃМ3ЃЉгыаТЭМЯѓгаСНИіЙЋЙВЕуЃЌЧвmЮЊећЪ§ЪБЃЌЧѓmЕФжЕЃЎ
x+mЃЈmЃМ3ЃЉгыаТЭМЯѓгаСНИіЙЋЙВЕуЃЌЧвmЮЊећЪ§ЪБЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉkЁм3ЃЛЃЈ2ЃЉyЃН2x2+4xЉ6ЃЌКЏЪ§ЭМЯѓМћНтЮіЃЛЃЈ3ЃЉmЃН1Лђ0ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнИљЕФХаБ№ЪНЁї=b2-4acКЭНЛЕуЕФИіЪ§ПЩжБНгЧѓНтЃЛ
ЃЈ2ЃЉИљОнЬтвтЧѓГіКЏЪ§ОЙ§ЕФЕуЃЈ-2ЃЌ-6ЃЉЃЌШЛКѓДњШыКЏЪ§ЕФНтЮіЪНМДПЩЧѓГіkЕФжЕЃЌДгЖјЕУЕНКЏЪ§ЕФНтЮіЪНЃЌЛГіЭМЯёЃЛ
ЃЈ3ЃЉИљОнЬтвтЛГіЗелКѓЕФЭМаЮЃЌИљОнЭМаЮЧѓГіСНИіНЛЕуЪБЕФЭМЯёЮЛжУЃЌЧѓГіmЕФМДПЩ.
ЃЈ1ЃЉИљОнЬтвтжЊb2Љ4acЃН16Љ8ЃЈkЉ1ЃЉЁн0ЃЌ
НтЕУЃКkЁм3ЃЛ
ЃЈ2ЃЉгЩЬтвтжЊ![]() ЃЌ
ЃЌ
Ёрx1+x2ЃНЉ2ЃЌ
ЁрХзЮяЯпЙ§ЕуЃЈЉ2ЃЌЉ6ЃЉЃЌ
НЋЃЈЉ2ЃЌЉ6ЃЉДњШыyЃН2x2+4x+kЉ1ЃЌЕУЃК8Љ8+kЉ1ЃНЉ6ЃЌ
НтЕУЃКkЃНЉ5ЃЌ
дђХзЮяЯпНтЮіЪНЮЊyЃН2x2+4xЉ6ЃЌ
ЦфКЏЪ§ЭМЯѓШчЯТЃК
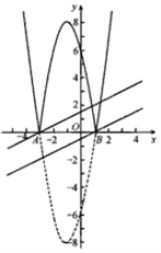
ЃЈ3ЃЉШчЭМЫљЪОЃЌЁпmЃМ3ЃЌ
ЁрЕБжБЯпЙ§ЃЈ1ЃЌ0ЃЉЪБЃЌжБЯпyЃН![]() x+mгыаТЭМЯѓга1ИіНЛЕуЃЌ
x+mгыаТЭМЯѓга1ИіНЛЕуЃЌ
ДЫЪБ![]() +mЃН0ЃЌМДmЃН-
+mЃН0ЃЌМДmЃН-![]() ЃЛ
ЃЛ
ЕБжБЯпЙ§ЃЈ-3ЃЌ0ЃЉЪБЃЌжБЯпyЃН![]() x+mгыаТЭМЯѓга3ИіНЛЕуЃЌ
x+mгыаТЭМЯѓга3ИіНЛЕуЃЌ
ДЫЪБ![]() +mЃН0ЃЌМДmЃН
+mЃН0ЃЌМДmЃН![]() ЃЛ
ЃЛ
НсКЯЭМаЮжЊЉ![]() ЃМmЃМ
ЃМmЃМ![]() ЃЌ
ЃЌ
ЁпmЮЊећЪ§ЃЌ
ЁрmЃН1Лђ0ЃЎ