题目内容
【题目】在数学课堂上,小斐同学和小可同学分别拿着一大一小两个等腰直角三角板,可分别记做![]() 和
和![]() ,其中
,其中![]() .
.
问题的产生:
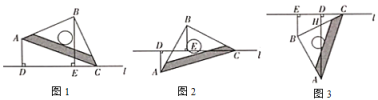
两位同学先按照如图摆放,点![]() 在
在![]() 上,发现
上,发现![]() 和
和![]() 在数量和位置关系上分别满足
在数量和位置关系上分别满足![]() ,
,![]() .
.
问题的探究:
(1)将![]() 绕点
绕点![]() 逆时针旋转一定角度.如图.点
逆时针旋转一定角度.如图.点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,连结
外部,连结![]() ,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
问题的延伸:
继续将![]() 绕点
绕点![]() 逆时针旋转.如图.点
逆时针旋转.如图.点![]() 都在
都在![]() 外部,连结
外部,连结![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() 点.
点.
(2)若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)成立 ,理由见解析;(2)①![]()
![]() ; ②
; ②![]() .
.
【解析】
(1)根据等腰直角三角形的性质解答;
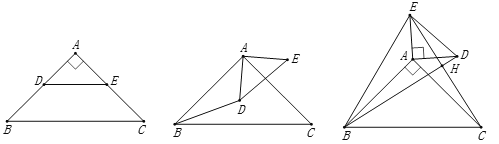
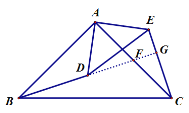
(2)延长BD,分别交AC、CE于F、G,证明△ABD≌△ACE,根据全等三角形的性质、垂直的定义解答;
(3)①根据S四边形BCDE=S△BCE+S△DCE计算,求出四边形BCDE的面积;②根据勾股定理计算即可.
(1)成立
理由如下:延长![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,
,
![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,
在![]() 和
和![]() 中,
中,
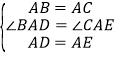 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,即
,即![]() ;
;
(2)①![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
②![]()
![]()
=![]()
![]()
![]() .
.

练习册系列答案
相关题目