��Ŀ����
����Ŀ���������Ǻ��������µĹ�ʽ��
sin����+�£�=sin��cos��+cos��sin���٣�cos����+�£�=cos��cos����sin��sin���ڣ�tan����+�£�=![]() ��
��
������Щ��ʽ�ɽ�ijЩ��������ǵ����Ǻ���ת��Ϊ����ǵ����Ǻ�������ֵ��
�磺tan105��=tan��45��+60�㣩=![]() =
=![]() =
=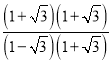 =����2+
=����2+![]() ����
����
���������֪ʶ�������ѡ���ʵ��Ĺ�ʽ��������ʵ�����⣺
��ͼ��ֱ���ɻ���һ������CD�Ϸ�A�㴦��ý����ﶥ��D��ĸ��Ǧ�=60�㣬��C��ĸ��Ǧ�=75�㣬��ʱֱ���ɻ��뽨����CD��ˮƽ����BCΪ42m��������CD�ĸߣ�
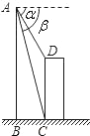
���𰸡�������CD�ĸ�Ϊ84�ף�
��������������������ɸ�����������ֵ��BC���AB�����ɸ�����������ֵ��BC���A��D���㴹ֱ���룮CD�ij��ɶ������������ã�
���������������=60������=75����BC=42��
��AB=BCtan��=42tan75��=42��![]() =42��
=42��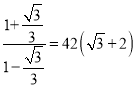 ��
��
A��D��ֱ����ΪBCtan��=42![]() ��
��
��CD=AB��42![]() =84���ף���
=84���ף���
�𣺽�����CD�ĸ�Ϊ84�ף�

��ϰ��ϵ�д�
�����Ŀ