题目内容
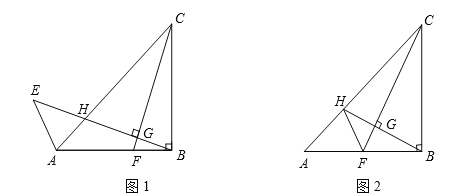
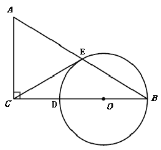
【题目】在 RtABC 中,ACB 90,点O在 BC 上,经过点 的⊙ O 与 BC ,AB 分别相交于点 D ,E 连接 CE , CE CA .
(1)求证: CE 是⊙ O 的切线;
(2)若 tan ABC ![]() ,BD 4,求CD 的长.
,BD 4,求CD 的长.
【答案】(1)见解析;(2) ![]() .
.
【解析】
(1) 连接OE,由CE=CA得∠A=∠CEA,由OE=OB得∠B=∠OEB,故∠CEA+∠OEB=90°,所以∠OEC =90°;
(2)设CD的长为![]() ,则BC=
,则BC=![]() +4,CO=2+
+4,CO=2+![]() ,由tan∠ABC=
,由tan∠ABC=![]() ,得AC=
,得AC=![]() BC=
BC=![]() (
(![]() +4) ,由CE=CA,得CE=
+4) ,由CE=CA,得CE=![]() (
(![]() +4) ,利用勾股定理得
+4) ,利用勾股定理得![]() .
.
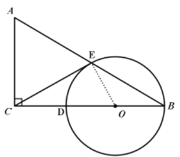
(1) 解:连接OE,
∵CE=CA,
∴∠A=∠CEA,
∵OE=OB,
∴∠B=∠OEB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠CEA+∠OEB=90°,
∴∠OEC =90°,
∴CE是⊙![]() 的切线
的切线
(2)设CD的长为![]() ,
,
∵BD=4,
∴BC=![]() +4,
+4,
CO=2+![]() ,
,
∵tan∠ABC=![]() ,
,
∴AC=![]() BC=
BC=![]() (
(![]() +4) ,
+4) ,
∵CE=CA,
∴CE=![]() (
(![]() +4)
+4)
在Rt△CEO中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CD的长为![]() .
.

练习册系列答案
相关题目