��Ŀ����
����Ŀ������̽����
�¶��壺
��һ��ƽ��ͼ�η�Ϊ�����ȵ������ֵ�ֱ�߽�����ƽ��ͼ�ε����Ȼ������������Ȼ���������ƽ��ͼ�νصõ��߶ν�����ƽ��ͼ�ε����Ȼ��߶���������Բ��ֱ������Բ�����Ȼ��߶�����
������⣺
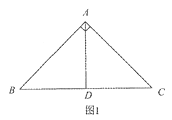
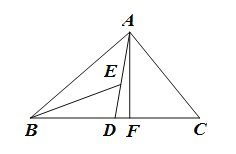
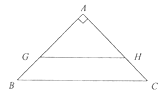
��֪��Rt��ABC�У���BAC=90����AB=AC=2![]() .
.
��1����ͼ1����AD��BC������ΪD����AD����ABC��һ���Ȼ��߶Σ�ֱ��д��AD�ij���
��2����ͼ2��ͼ3�У��ֱ�һ���Ȼ��߶Σ���ֱ��д�����ǵij���. ��Ҫ��ͼ1��ͼ2��ͼ3�еĵȻ��߶εij��ȸ�����ȣ�
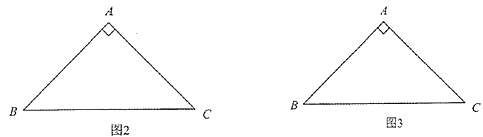
���𰸡���1��AD=2����2�����������ͼ�μ�������BE=![]() ��GH=2
��GH=2![]()
�������������������1�����ݵ���ֱ�������ε����ʣ��ױ��ϵĸ�������ã�
��2��������BE������BE��Ϊһ���Ȼ��ߣ����ù��ɶ���������ó��ȣ�
��GH//BC��GH��Rt��ABC�������Ϊ��ȵ����ݣ���GH��Ϊһ���Ȼ��ߣ��������������ε����ʼ�����ó���.
�����������1����Rt��ADC��
��AC=2![]() ����C=45����
����C=45����
��AD=2��
��2�����������ͼ��������ʾ��
EΪAC�е㣬����AE=![]() ,
,
��Rt��ABE�У����ݹ��ɶ����ɵ�BE=![]() =
=![]() ��
��
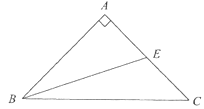
GH��BC��S��AGH=![]() S��ABC��
S��ABC��
��GH//BC�����AGH����ABC��
��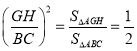 ��
��
�ߡ�A=90����AB=AC=![]() ����BC=
����BC=![]() =4��
=4��
��![]() ��
��
��GH=2![]() .
.

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�����Ŀ��2019��4��23�գ���24����������գ�Ϊ���ƽ��л���ͳ�Ļ�������Ӫ��Ũ���Ķ����Χ������ijѧУ�ٰ��ˡ��ö����Ϊϰ�ߣ�������Ʈ��У��������Ϊ����Ϊÿ���༶������һ���µ�ͼ�飬��һ�꼶�����ඩ��ͼ��������±���

�����ļ����ף� | �Ĵ����ƣ��ף� | �ܱ��ã�Ԫ�� | |
��һ��1���� | 4 | 2 | 80 |
��һ��2���� | 2 | 3 | 520 |
��1���������ļ����Ĵ�����ÿ���Ƕ���Ԫ��
��2��ѧУ���ٹ��������ļ����Ĵ�������10�ף��ܷ��ò�����700Ԫ����ѧУ���ļ��ֹ�����
����Ŀ��ijѧУ����־Ը��Э��Ը��г����Ŀ����������е��飬��ȫ��365���������ȡ��80��Ŀ�������ָ����AQI�����ݣ����Ƴ�������������ͳ��ͼ���������ͼ�����ṩ����Ϣ����������⣺
AQIָ�� | �����ȼ� | �������죩 |
0��50 | �� | m |
51��100 | �� | 44 |
101��150 | �����Ⱦ | n |
151��200 | �ж���Ⱦ | 4 |
201��300 | �ض���Ⱦ | 2 |
300���� | ������Ⱦ | 2 |
��1 ��ͳ�Ʊ���m= ��n= ������ͳ��ͼ�У����������ȼ�Ϊ������������ռ %��
��2����ȫ����ͳ��ͼ����ͨ��������Ƹ��г���ȫ����������ȼ�Ϊ���������������������������죿
��3���ݵ��飬������Ⱦ��2�췢���ڴ����ڼ䣬ȼ���̻������Ϊ������Ⱦ��һ����Ҫԭ�ݴˣ��������һ�����������飮