题目内容
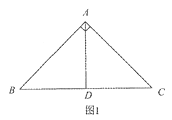
【题目】如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当t=0.5时,求线段QM的长;
(2)当M在AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形?若可以,请求t的值;若不可以,请说明理由.
(3)当t>2时,连接PQ交线段AC于点R.请探究![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.



【答案】(1)QM=1;(2)t=1或![]() 或4;(3)
或4;(3)![]() 为定值,
为定值, ![]() .
.
【解析】试题分析:(1)过点C作CF⊥AB于F,利用直线平行得出Rt△AQM∽Rt△ACF,再利用对应边的比值相等求出即可;
(2)由于∠DCA为锐角,故有三种情况:
①当∠CPQ=90°时,点P与点E重合,可得DE+CP=CD,从而可求t;②当∠PQC=90°时,如备用图1,容易证出Rt△PEQ∽Rt△QMA,再利用比例线段,结合EQ=EM﹣QM =4-2t,可求t;③当P在AD上时,∠PCQ=90°,此时PD=CD,代入即可求出t的值;
(3)当t>2时,如备用图2,先证明四边形AMQP为矩形,再利用平行线分线段成比例定理的推论可得△CRQ∽△CAB,再利用比例线段可求![]() .
.
试题解析:
解:(1)过点C作CF⊥AB于F,则四边形AFCD为矩形.
∴CF=4,AF=2,
此时,Rt△AQM∽Rt△ACF,
∴![]() ,
,
即![]() ,
,
∴QM=1;
(2)根据题意可得当0≤t≤2时,以C、P、Q为顶点可以构成三角形为直角三角形,故有三种情况:
①当∠CPQ=90°时,点P与点E重合,此时DE+CP=CD,即t+t=2,∴t=1;
②当∠PQC=90°时,
如备用图1,此时Rt△PEQ∽Rt△QMA,
∴![]() ,
,
由(1)知,EQ=EM﹣QM=4﹣2t,
而PE=PC﹣CE=PC﹣(DC﹣DE)=t﹣(2﹣t)=2t﹣2,
∴![]() ,
,
∴t=![]() ;
;
③当P在AD上时,∠PCQ=90°,此时PD=CD,所以t-2=2 ,所以t=4;
综上所述,t=1或![]() 或4;
或4;
(3)![]() 为定值,
为定值,
当t>2时,如备用图2,PA=DA﹣DP=4﹣(t﹣2)=6﹣t,
由(1)得,BF=AB﹣AF=4,∴CF=BF,∴∠CBF=45°,∴QM=MB=6﹣t,∴QM=PA,
∵AB∥DC,∠DAB=90°,∴四边形AMQP为矩形,∴PQ∥AB,∴△CRQ∽△CAB,
∴![]() .
.