Question

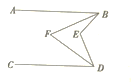
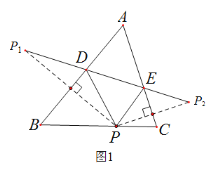
【题目】（1）如图1，在△ABC中，∠A，P是BC边上的一点，，是点P关于AB、AC的对称点，连结，分别交AB、AC于点D、E.

①若，求的度数；

②请直接写出∠A与的数量关系：___________________________；

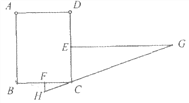
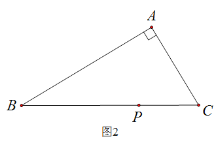
（2）如图2，在△ABC中，若∠BAC，用三角板作出点P关于AB、AC的对称点、，（不写作法，保留作图痕迹），试判断点，与点A是否在同一直线上，并说明理由.

Answer 1

【答案】（1）64°；（2）∠DPE=180°-2∠A；（3）在．

【解析】（1）①由轴对称的性质以及四边形内角和为360°可得：∠DPP1+∠DPE+∠EPP2+∠A=180°（i），由三角形外角的性质以及三角形内角和为180°得到2∠DPP1+∠DPE+2∠EPP2=180°（ii），解方程组即可得到结论

（2）由①得∠DPP1+∠DPE+∠EPP2+∠A=180°（i），2∠DPP1+∠DPE+2∠EPP2=180° （ii），解方程组即可得到结论．

（3）连接AP、AP1、AP2．根据轴对称的性质，可得：∠4=∠1，∠3=∠2， 由∠BAC=90°，得到∠3+∠4=90°，即有∠1+∠2+∠3+∠4=180°，从而得到结论．

（1）①∵点P、点P1关于直线AB对称，点P、点P2关于直线AC对称，∴PD=P1D，PE=P2E，∴∠P1=∠DPP1，∠P2=∠EPP2，∴∠EDP=2∠DPP1，∠DEP=2∠EPP2，∠DPP1+∠DPE+∠EPP2+∠A=180°（i）

∵2∠DPP1+∠DPE+2∠EPP2=180° （ii）

（ii）—（i）得：∠DPP1+∠EPP2=∠A，

又∵∠A=58°，∴∠DPP1+∠EPP2=58°，

∴∠DPE=64°

（2）∠DPE=180°－2∠A ．理由如下：

由①得：∠DPP1+∠DPE+∠EPP2+∠A=180°（i）

2∠DPP1+∠DPE+2∠EPP2=180° （ii）

（i）×2－（ii）得：2∠A－∠DPE=180°，

∴∠DPE=180°－2∠A ．

（3）点P1，A，P2在同一条直线上．理由如下：

连接AP、AP1、AP2．

根据轴对称的性质，可得：∠4=∠1，∠3=∠2，

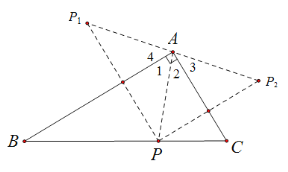
∵∠BAC=90°，即∠1+∠2=90°，

∴∠3+∠4=90°，

∴∠1+∠2+∠3+∠4=180°，

即∠P1AP2=180°，

∴点P1 、A、P2在同一条直线上．