题目内容
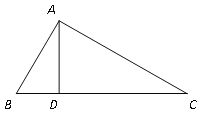
【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
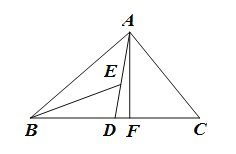
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
【答案】(1)60°;(2)8
【解析】
(1)先利用三角形的外角性质计算出∠ABE=15°,再利用角平分线定义得到∠ABC=2∠ABE=30°,然后根据高的定义和互余可求出∠BAF的度数;
(2)先根据中线定义得到BC=2BD=10,然后利用三角形面积公式求AF的长.
(1)∵∠BED=∠ABE+∠BAE,
∴∠ABE=40°-25°=15°,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=30°,
∵AF为高,
∴∠AFB=90°,
∴∠BAF=90°-∠ABF=90°-30°=60°;
(2)∵AD为中线,
∴BD=CD=5,
∵S△ABC=![]() AFBC=40,
AFBC=40,
∴AF=![]() =8.
=8.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目